x3+x−2=0
x3+x−2=0Ищем первый корень через делители числа -2.
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2Очевидно, что корень будет x=1
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2Очевидно, что корень будет x=1Далее делим в столбик начальное выражение на корень уравнения (x-1)
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2Очевидно, что корень будет x=1Далее делим в столбик начальное выражение на корень уравнения (x-1)Получаем результат x^{2}+x+2x2+x+2 .
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2Очевидно, что корень будет x=1Далее делим в столбик начальное выражение на корень уравнения (x-1)Получаем результат x^{2}+x+2x2+x+2 .Приравниваем его к нулю, видим, что корней нет, так как дискриминат отрицательный.
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2Очевидно, что корень будет x=1Далее делим в столбик начальное выражение на корень уравнения (x-1)Получаем результат x^{2}+x+2x2+x+2 .Приравниваем его к нулю, видим, что корней нет, так как дискриминат отрицательный.Следовательно, ответ: x=1
Объяснение:
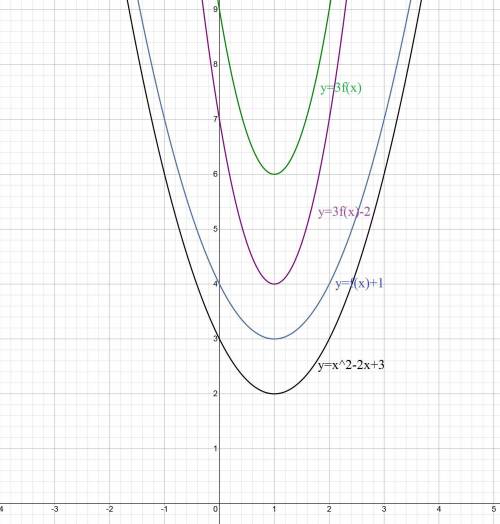
Строим график функции f(x)=x²– 2x+3
x₀=-b/(2a)=2/2=1
y₀=1-2+3=2
Ветви направлены вверх.
х у
0 3
2 3
1) у=f(x)+1
Это означает, что график смещается на 1 вверх по оси ОУ.
Смещаем график. Значит вершина будет в точке (1; 3)
2) у = 3f(х);
Это означает, что график сжимается в 3 раза вдоль оси OX.
Вершина остается в той же точке х₀=1, а вот значение увеличится в 3 раза: у₀=2*3=6.
3) у = 3f(x) – 2
График, построенные в п. 2) смещаем на 2 вниз относительно оси ОУ.
При этом вершина окажется в точке (1; 4)
D(y)∈(-∞;-1) U (-1;∞)
x=-1-вертикальная асимптота
y(-x)=(-2x-3)/(-x+1) ни четная ,ни нечетная
(0;-3);(1,5;0)-точки пересечения с осями
y`=(2x+2-2x+3)/(x+1)²=5/(x+1)²>0 при всех принадлежащих области определения функция возрастает
х -3 -2 3 4
у 4,5 7 3/4 1