Вычислить: 1) 2 умножить на 36 в степени одна вторая 2) 27 в степени минус одна третья вырожение: 1) а в степени минус одна вторая умноженное на а в степени три четвертых 2) с в степени две третьих умноженное на с в степени одна вторая в числителе и с в степени одна шестая в знаменателе 3)скобочка открывается х в сепени одна третья скобочка закрывается все это в минус треьей степени умноженное на х степени две третьих сократите дробь: 1) б плюс 7б в степени одна вторая в числителе и 7 плюс б в степени одна вторая в знаменателе 2) 3 плюс а в степени одна вторая в числителе и а минус 9 в знаменателе
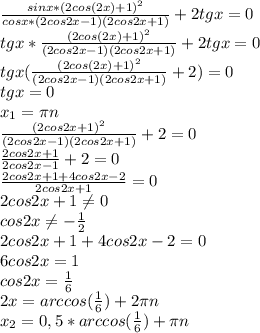
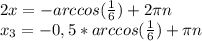
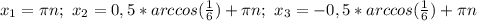
2)19683
3)а в степени -одна вторая+степень три четвертых=а в степени одна четвертая
4)с в степени две третьих+степень одна вторая- одна шестая=с в степени 1=с
5)х в степени минус одна третья
сократить дробь:
1)возможно б делить на 7
2)один делить на корень из а минус 3