а = 9
Объяснение:
При каком значении а
графики функций
у=3х+4 и
у= - 2х + а
пересекаются в точке с абсциссой 1
Ось абсцисс - это ось Ох, значение абсциссы показывает значение координаты "х"
т.е. точка с абсциссой 1 - это точка А(1; у), где координата х известна.
Точка(-и) пересечения графиков ф-ий - это решения системы уравнений, в данном случае такой:
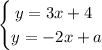
Известно, что х = 1. Подставим значение в систему:
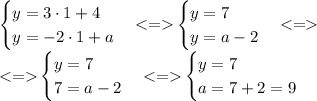
Отсюда получаем:
То есть - при значении
a = 9
графики функций
у=3х+4
у= - 2х + а
пересекаются в точке с абсциссой 1.
И это точка с координатами (1; 7)
Объяснение:
1) 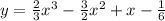
1а. критические точки определяются как производная первого порядка
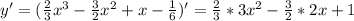
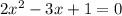
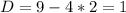
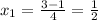 ;
; 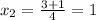
 ;
; 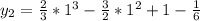
 ;
; 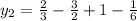
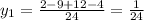 ;
; 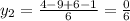
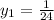 ;
; 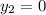
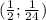
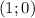
выпуклость ( вторая производная )
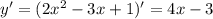
4x -3 =0
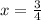 ;
; 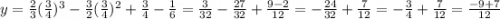
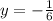
( 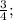
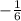 )
)
и так с каждой функцией сделаешь по аналогии...
2) 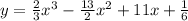
3) 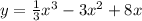
4 ) 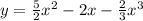
5) 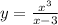
6) 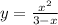
X^2 + 3x - ( 1 - 2x^2 ) = 3x^2 - x + 4
X^2 - 3x - 1 + 2x^2 = 3x^2 - X + 4
3x^2 - 3x - 1 = 3x^2 - X + 4
- 3x + X = 4 + 1
- 4x = 5
X = - 1,25
ОТВЕТ ( - 1,25 )
N 2
X^2 - 5x + 5 = - x^2 - x - ( - 3 - 2x^2 )
X^2 - 5x + 5 = - x^2 - X + 3 + 2x^2
X^2 - 5x + 5 = x^2 - X + 3
- 5x + X = 3 - 5
- 4x = - 2
X = 0,5
ОТВЕТ 0,5
N 3
- 2x^2 + 4x - 7 = - x^2 + 2x - ( x^2 - 3 )
- 2x^2 + 4x - 7 = - x^2 + 2x - x^2 + 3
- 2x^2 + 4x - 7 = - 2x^2 + 2x + 3
4x - 2x = 3 + 7
2x = 10
X = 5
ОТВЕТ 5