1) x ∈ (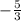
, 1)
2) x ∈ (-∞, 2] U [4, +∞)
3) x ∈ (-∞, 2) U (3, +∞)
4) x ∈ (-4, 1)
Объяснения:
1) |3x + 1| < 4.
Рассмотрим возможные случаи:
[ 3x + 1 < 4, 3x + 1 ≥ 0 [ x < 1, x ≥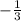 
| ⇔ |
[ - (3x + 1) < 4, 3x + 1 < 0 [ x > 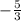, x <
[ x 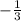∈ [, 1) [
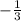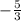| ⇔ | x ∈ (, 1)
[ x ∈ (, ) [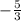
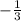2) |2x - 5| ≥ x - 1
|2x - 5| - x ≥ -1
Рассмотрим возможные случаи:
[ 2x - 5 - x ≥ - 1, 2x - 5 ≥ 0 [ x ≥ 4, x ≥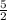 
| ⇔ |
[ - (2x - 5) - x ≥ -1, 2x - 5 < 0 [ x ≤ 2, x <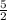
[ x ∈ [4, +∞) [
| ⇔ | x ∈ (-∞, 2] U [4, +∞)
[ x ∈ (-∞, 2] [
3) |5 - 2x| > 1
Рассмотрим возможные случаи:
[ 5 - 2x > 1, 5 - 2x ≥ 0 [ x < 2, x ≤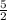
| ⇔ |
[ - (5 - 2x) > 1, 5 - 2x < 0 [ x > 3, x >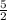
[ x ∈ (-∞, 2) [
| ⇔ | x ∈ (-∞, 2) U (3, +∞)
[ x ∈ (3, +∞) [
4) |x| + |x + 3| < 5
Рассмотрим возможные случаи:
[ x + x + 3 < 5, x ≥0, x + 3 ≥ 0 [ x < 1, x ≥ 0, x ≥ -3
[ -x + x + 3 < 5, x < 0, x + 3 ≥ 0 [ x ∈ R, x < 0, x ≥ -3
| ⇔ |
[ x - (x + 3) < 5, x ≥ 0, x + 3 < 0 [ x ∈ R, x ≥ 0, x < -3
[ -x - (x+3) < 5, x <0, x + 3 < 0 [ x > -4, x < 0, x < -3
[ x < 1, x ∈ [0, +∞) [ x ∈ [0, 1) [
[ x ∈ R, x ∈ [-3,0) [ x ∈ [-3, 0) [
| ⇔ | ⇔ | x ∈ (-4, 1)
[ x ∈ R, x ∈ ∅ [ x ∈ ∅ [
[ x > -4, x ∈ (-∞, 3) [ x ∈ (-4, -3) [
Объяснение:
Пусть х км/ч-скорость по течению и у км/ч-скорость лодки против течения.
За 3 ч по течению лодка х км,за 4 ч.против течения-4у км,а вместе:
3х+4у=114 км(по условию задачи).Кроме того ,за 5 ч по течению проплыла столько же,сколько за 6ч против течения,то есть:5х=6у.То есть получаем систему уравнений:
3х+4у+114·l5l, 15x+20y=570
5х=6у ·l3l, 15x=18y,
18y+20y=570, 38y=570,y=570:38,
у=15(км/ч)-скорость лодки против течения
5х=15·6,5х=90,х=90:6,
х=18(км/ч)-скорость лодки по течению реки
х*v=900
(х-1)*(v+10)=900
xv-v+10x-10=900
Подставим вместо xv 900:
900-v+10x=910
Выразим х и подставим:
900-v+9000/v=910 |*v
900v-v²+9000=910v
v²+10v-9000=0
D=190²
v1=90 v2=-100(не удовлетворяет, отриц)
х=900/v=900/90=10