Докажите что значение дроби равно ноль (1,24-1 1/25) * 2,5 - 1/6 : 1/3 разделить(дробная черта) 1,4 : 0,1 - 2

👇

Ответ:

НВТула

23.03.2020

Числитель
1) 1,24 - 1 1/25 = 1,24 - 1,04 = 0,2
2) 0,2 • 2,5 = 0,5
3) 1/6 : 1/3 = 3/6 = 1/2 = 0,5
4) 0,5 - 0,5 = 0
2) если числитель равен нулю, то и вся дробь равна нулю

4,8(68 оценок)

Открыть все ответы

Ответ:

barinova6

23.03.2020

1) х³ + х² - 6 * х = 0

х * (х² + х - 6) = 0

х₁ = 0 х₂ = 2 х₃ = -3

2) (x² - 2x + 3)(x² - 2x + 4) = 6

пусть х² - 2*х + 3 = т. уравнение принимает вид

т * (т + 1) = 6

т² + т - 6 = 0

т₁ = -3 т₂ = 2

1) х² - 2 * х + 3 = 2

х² - 2 * х + 1 = (х - 1)² = 0

х = 1

2) х² - 2 * х + 3 = -3

х²- 2 * х + 6 = 0

корней нет (дискриминант отрицательный)

3) 6*x² + 11*x - 2 = 0 6*x - 1

уравнение 6*x² + 11*x - 2 = 0 имеет 2 корня: х₁ = -2 х₂ = 1/6

второй корень не подходит, так как в этом случае знаменатель равен нулю

4,8(82 оценок)

Ответ:

anastasia69smirnova

23.03.2020

1.-4cos(x)+C(тут и подробно ну нужно, ибо тупо по формуле ну и -4 за знак интеграла)
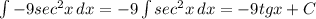
2. $\int{-9 sec^2x} \, dx =-9 \int{sec^2x} \, dx = -9 tgx+C$
представил 1/cosx как secx
3.6sinx (аналогично первому)
4. ну тут аналогично второму, сначала представим 1/sinx, как cosecx и получим:
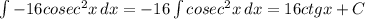
$\int {-16cosec^2x} \, dx =-16 \int {cosec^2x} \, dx = 16ctgx+C$
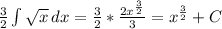
5. $\frac{3}{2} \int { \sqrt{x} } \, dx =\frac{3}{2}* \frac{2x^ \frac{3}{2} }{3} =x^ \frac{3}{2}+C$
6. аналогично по формуле,-15 выносим за знак интеграла, 1/x^2=-1/x,
получаем -15*(-1/x)=15/x+C
7. выносим 5/2 за знак интеграла и раскрываем интеграл, используя формулу:
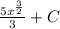получаем: $\frac{5x^ \frac{3}{2} }{3} +C$ \
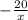
8. устал одно и тоже писать, выносим -20 за знак интеграла, применяем формулу и получаем: $- \frac{20}{x}$
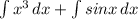
9. разобьем на два интеграла: $\int{x^3} \, dx + \int{sinx} \, dx$
применим формулы для двух интегралов и получим:
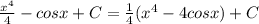
$\frac{x^4}{4}-cosx+C= \frac{1}{4}(x^4-4cosx)+C$
10. опять же, представим 1/cosx=secx, затем разобьем на два интеграла и получим:
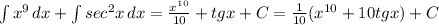
$\int{x^9} \, dx + \int{sec^2x} \, dx= \frac{x^{10}}{10}+tgx+C= \frac{1}{10} (x^{10}+10tgx)+C$
11. эхх, устал...
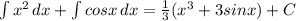
$\int {x^2} \, dx + \int {cosx} \, dx = \frac{1}{3}(x^3+3sinx)+C$
12. аналогично десятому.
представляем 1/sinx=cosec x, разбиваем на два интеграла и используем формулы, получаем:
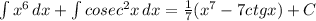
$\int {x^6} \, dx + \int {cosec^2 x} \, dx= \frac{1}{7}(x^7-7ctgx)+C$