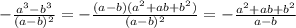
скорость моторной лодки от пристани до острова равна 50 км/ч.
1. x км/ч – скорость, с которой моторная лодка плыла от пристани до острова.
2. Составляем уравнение.
150 / x = 150 / (x + 10) + 0,5;
150 / x – 150 / (x + 10) = 0,5;
(150 * (x + 10) – 150x) / (x^2 + 10x) = 0,5;
(150x + 1500 – 150x) / (x^2 + 10x) = 0,5;
1500 = 0,5 * (x^2 + 10x);
0,5x^2 + 5x – 1500 = 0;
x^2 + 10x – 3000 = 0;
Дискриминант = 10 * 10 + 4 * 1 * 3000 = 12100 (корень из 12100 равен 110)
x = (-10 + 110) / 2 или x = (-10 - 110) / 2;
x ¹ = 50 или x = -60;
²
Так как скорость не может быть отрицательной, то она равна 50 км/ч.
a) (x+2)+(x - 2)= x+2+x - 2=2х - раскрыли скобки, т.е. просто опустили и привели подобные.
б) (2x - 3y)*(2x +34)=4х²+68х-6ху-102у
в) (b² +4)*(4-b²)=(4+b² )*(4-b²)=4²-(b²)²=16-b⁴- при возведении степени в степень мы перемножаем показатели. как здесь 2*2=4.
г) (y+3)*(y-3)=у²-9
д) (3a-3y)*(2x+3y)=6ах+9ау-6ху-9у²
е) (b²+4)*(4-b²)=) (4+b²)*(4-b²)=16-b⁴
в номерах в), г), е) использовали формулу разности квадратов. т.е.
(а-с)*(а+с)=а²-с², в остальных б) , д), просто раскрывали скобки по распределительному закону, т.е. умножали все члены первой скобки на все члены второй