x⁴ - 3x² - 4 = 0
x² = t
t² - 3t - 4 = 0
d = 9 + 16 = 25
x² = -1
нет корней
x² = 4
x₁ = 4
x₂ = -4
ответ: x = 4; -4
1 б(x² - 1)(x² + 4x + 3) = 0
x² + 4x + 3 = 0
d = 16 - 12 = 4
ответ: x = 1; -1; -3
2воспользуемся свойством пропорции:
x² - 4 = 0
x² = 4
x = ±4
ответ: x = 4; -4
2 бвоспользуемся свойством пропорции:
x² - 3x - 10 = 0
d = 9 + 40 = 49
ответ: x = -2; 5
2 вответ: x = 1; -4
3(x² + 2x)² + 13(x² + 2x) + 12 = 0
x² + 2x = t
t² + 13t + 12 = 0
d = 169 - 48 = 121
x² + 2x = -12
x² + 2x + 12 = 0
d = 4 - 48 = -44
нет корней
x² + 2x = -1
x² + 2x + 1 = 0
d = 4 - 4 = 0
ответ: x = -1
прости, с 4-ым не смогу .
Пусть х км/ч - скорость, с которой Иван ехал на велосипеде, тогда x+30 км/ч - скорость, с которой Иван ехал на автомобиле. На велосипеде Иван проехал 24 км, а на автомобиле 84 км за это же время.
24/x ч - время, за которое Иван проехал 24 км на велосипеде.
84/(x+30) ч - время, за которое Иван проехал 84 км на автомобиле.
Составим уравнение (помним, что время одинаковое):
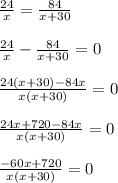
ОДЗ: x≠0; x≠-30 (т.к. на 0 делить нельзя)
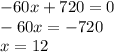
12 км/ч - скорость, с которой Иван ехал на велосипеде.
24/12=2 ч - за это время Иван проехал 24 км на велосипеде.
А т.к. время равно, что за первое расстояние, что за второе расстояние, то и за 2 ч Иван проехал 84 км на автомобиле.
ответ: 12 км/ч; 2 ч

синус не накладывает никаких ограничений. Поэтому область определения вся числовая прямая.