1. у=4х-2
1)
х=0 у=4*0-2=-2
х=6 у=4*6-2=10
2)
у=0
4х-2=0
4х=2
х=0,5
у=2
4х-2=2
4х=4
х=1
2.
Пересечение с осью ОХ:
у=0
1,2х-24=0
1,2х=24
х=20
(20; 0)
Пересечение с осью ОУ:
х=0
у=1,2*0-24
у=-24
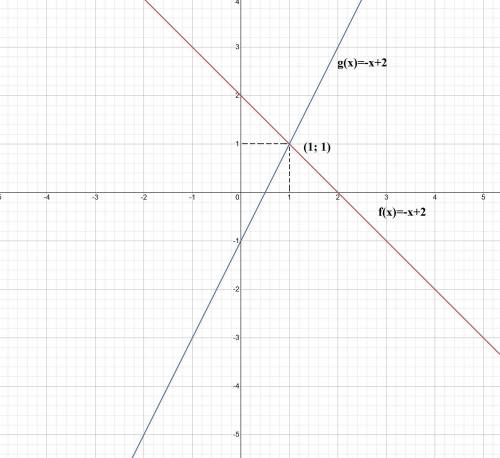
3. Поскольку оба графика линейные функции, то для построения достаточно 2х точек:
f(x)=-x+2
x y
0 2
1 1
g(x)=2x-1
x y
0 -1
2 3
1) Из графика видно, что точка пересечения (1; 1)
2) Из построенных графиков видно, что g(x)>f(x), при х>1.
4. График линейной функции имеет вид:
у=kx+b
a График проходит через точки (0; 0), (1; 1)
0=k*0+b ⇒b=0
1=k*1 ⇒k=1
у=х
б) Графиком является постоянная функция:
у=-2
в) График проходит через точки (0; 3) и (3;0)
3=0*k+b ⇒b=3
0=3k+b
3k=0-3
k=-1
y=-x+3
1. у=4х-2
1)
х=0 у=4*0-2=-2
х=6 у=4*6-2=10
2)
у=0
4х-2=0
4х=2
х=0,5
у=2
4х-2=2
4х=4
х=1
2.
Пересечение с осью ОХ:
у=0
1,2х-24=0
1,2х=24
х=20
(20; 0)
Пересечение с осью ОУ:
х=0
у=1,2*0-24
у=-24
3. Поскольку оба графика линейные функции, то для построения достаточно 2х точек:
f(x)=-x+2
x y
0 2
1 1
g(x)=2x-1
x y
0 -1
2 3
1) Из графика видно, что точка пересечения (1; 1)
2) Из построенных графиков видно, что g(x)>f(x), при х>1.
4. График линейной функции имеет вид:
у=kx+b
a График проходит через точки (0; 0), (1; 1)
0=k*0+b ⇒b=0
1=k*1 ⇒k=1
у=х
б) Графиком является постоянная функция:
у=-2
в) График проходит через точки (0; 3) и (3;0)
3=0*k+b ⇒b=3
0=3k+b
3k=0-3
k=-1
y=-x+3

a³² * a⁴³ = a³²⁺⁴³ = a⁷⁵. Следовательно данное высказывание является общим и истинным.
б) ∃ а ∈ Q, a≠0: a³²*a⁴³=2a⁷⁵ - это значит, что существует хотя бы одно рациональное число a, которое удовлетворяет условию: a³²*a⁴³=2a⁷⁵
Если a = 0, то 0³² * 0⁴³=2*0⁷⁵ ⇔ 0 = 0. Вывод: высказывание является истинным. Это высказывание о существовании.
в)∀ a ∈ Q: a³²*a⁴³= a³²+a⁴³ - для всех рациональных a верно следующее равенство. Так как a³²*a⁴³ > a³²+a⁴³ (на множестве (-∞;0)∪(0;+∞) - значит высказывание ложно(оно может быть верно лишь в случае, когда a = 0.) Это общее высказывание.
г) ∀ n ∈ N: 28ⁿ=7ⁿ+4ⁿ - для всех натуральных n верно следующее. Высказывание неверно, потому что 28ⁿ > 7ⁿ+4ⁿ (при n∈R). Данное утверждение - общее высказывание.
д) ∀ n ∈ N: 28ⁿ=7ⁿ*4ⁿ - при всех натуральных n равенство справедливо. 28ⁿ = 7ⁿ * 4ⁿ ⇔ 28ⁿ = 28ⁿ - означает, что высказывание общее и верное.