Для бинома
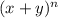
справедливы следующие утверждения:
1. Степени x начинаются со степени бинома n и уменьшаются до 0; степени y начинаются с 0 и увеличиваются до n. Последний член не имеет множителя x. Первый член не имеет множителя y, т.е.
2. Коэффициенты начинаются с 1 и увеличиваются на определенные значения (до среднего члена), а потом уменьшаются на те же значения обратно к 1.
3. Бином содержит n+1 членов
4. k-ый член можно найти следующим образом:
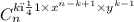
5. Средний член в биноме чётной степени находится по формуле:
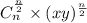
На основе теории решим данную задачу:
a) 4 + 1 = 5
b) 3. коэффициент этого члена выглядит так:
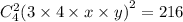
с) Из предыдущего пункта:
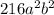
Примечание: Коэффициент при члене ab³ для данного бинома также равен 216
Cоставим уравнение касательной к кривой в точке z
y(z)=√(z+2);
y`(x)=1/2√(x+2)
y`(z)=1/2√(z+2)
Уравнение
у-у(z)=y`(z)(x-z)
y-√(z+2)=(x-z)/2√(z+2)
Найдем точки пересечения касательной с осями координат
При х=0 у=√(z+2)-(z/2√(z+2))=(2z+4-z)/2√(z+2)=(z+4)/2√(z+2)
При у=0 x-z=-2(z+2) ⇒x=-z-4
Треугольник, образуемый касательной с осями координат- прямоугольный, с катетами |-z-4| и |(z+4)/2√(z+2)|
Площадь прямоугольного треугольника находим по формуле как половину произведения катетов:
S(Δ)=(1/2)|-z-4|·(z+4)/2√(z+2)=(z+4)²/4√(z+2)
S`(z)=2(z+4)(3z+4)/16(z+2)√(z+2)
S`(z)=0
3z+4=0
z=-4/3
y(-4/3)=√((-4/3)+2)=1/√3
О т в е т.(-4/3; 1/√3)