Если квадратное уравнение имеет одинаковые корни, то это значит, что оно имеет один корень. Один корень квадратное уравнение имеет в том случае, когда дискриминант равен 0. Поэтому нам надо найти дискриминант и приравнять его к нулю.
(3b + 5 )х² - 2(b - 1)x + 2 = 0;
D = b^2 - 4ac - коэффициенты a, b и c равны a = 3b + 5; b = - 2(b - 1); c = 1;
D = (- 2(b - 1))^2 - 4 * (3b + 5 ) * 2 = 4(b^2 - 2b + 1) - 8(3b + 5) = 4b^2 - 8b + 4 - 24b - 40 = 4b^2 - 32b - 36;
4b^2 - 32b - 36 = 0 - поделим почленно на 4;
b^2 - 8b - 9 = 0;
D = (- 8)^2 - 4 * 1 * (- 9) = 64 + 36 = 100; √D = 10;
x = (- b ± √D)/(2a);
b1 = (8 + 10)/2 = 9;
b2 = (8 - 10)/2 = - 1.
По условию нам нужен отрицательное значение b, поэтому в ответ записываем только отрицательный корень.
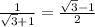
Вспомним формулу корней. У нее в знаменателе 2a. А у нас 2. Тогда хорошо бы было, если a=1.
Дальше, запишем наш корень так: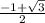 
. Опять же, глядя на формулу, хорошо будет, если b=1. Теперь подберем последний коэффициент c так, чтобы дискриминант был равен числу 3. Коэффициенты a и b известны, поэтому запишем формулу дискриминанта: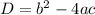 
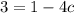
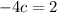
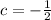
Не получилось немного.. коэффициент у нас не целый-то! Но насчет квадратного уравнения хорошо то, что если мы умножим все члены на любое отличное от нуля число, то корни не изменятся.
Из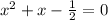 
мы получаем равносильное относительно корней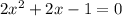 
Теперь все коэффициенты целые!
2)2*(17+8)=50дм=500 см
не забудь поблагодарить меня