Для решение системы уравнений
x - 4y = 9;
3x + 2y = 13,
нужно использовать метод алгебраического сложения. Начнем мы с того, что умножим второе уравнение системы на 2 и получим:
x - 4y = 9;
6x + 4y = 26;
Сложим почленно два уравнения системы и получим уравнение:
6x + x = 9 + 26;
2y = 13 - 3x.
Из первого уравнения системы ищем переменную x:
x(6 + 1) = 35;
7x = 35;
x = 35 : 7;
x = 5.
Система уравнений:
x = 5;
y = (13 - 3x)/2;
Подставляем значения во второе уравнение:
x = 5;
y = (13 - 3 * 5)/2 = (13 - 15)/2 = -2/2 = -1.
ответ: (5; -1).
Объяснение:
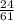проте ймовірність того, що листок містить саме число 2 менша та дорівнює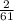 
Объяснение:
У високостном році 366, є місяці по 31 денів по 30 днів та у лютому 29 днів
Тож подивимось скількі днів у місяці містять двійку:
це номери 2, 12, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29 - загалом це 12 днів на місяць,
як бачимо у кожному місяці високостного року по 12 днів із цифрою 2
тому на рік таких днів буде 12*12=144
а ймовірність такої події 
--------------------------
якщо ж казати про можливість натрапити саме на число 2 на листочку то це лише 
, оскыльки других днів у році стількиж скіль ки ж і місяців у році, а саме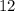 
и набольшее число будет х+4 т.е. 12400+4=12405
обяснение: округляем до большего при (х)5 к (х+1)0
а также те, что меньше (х)4 к (х)0
например: 120к120, 121к120 124к120, 125к130129к130 и т.д.