Сначала выполняем действия в скобках: 8² • 8³ =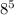 
(по свойству степени: при умножении чисел со степенями, показатели степеней складываются)
Далее возводим в квадрат:.( 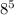)² = 
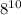(по свойству степени: при возведении степени в степень показатели степеней перемножаются)
ответ: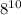
Удачи))
Кол-во таких чисел=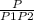
.
Здесь P -общее кол0во перестановок 6 чисел : P=6!=60*12
P1 - число перестановок цифры 1 в этом числе. То есть мы как бы путем деления общего числа перестановок на число перестановк конкретной цифры убираем повторяющиеся перестановки, образуемые этой цифрой. Так как кол-во единиц в наборе 2 штуки, то
P1=2!=2
Аналогично для P2=3!=6
P=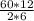 
=60.
если бы например в наборе были бы только единицы напрмиер, то получилось бы единственное возможное число, что доказывает некоторую универсальность моей формулой
Нужно умножить все ступени в скобках на 2. И получается 8^4•8^6.
При умножении степеней с одинаковым основанием ,основание переписывается,а степени суммируются. 8^6+4=8^10