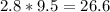
а)(53+27)²=80²=6 400
б)(186-76)²=110²=12 100
в)735²+2·735·728+728²-4·735·728=
=735²-2·735·728+728²=(735-728)²=7²=49
г) (744-740)²=4²=16
д)(306+694)²=1 000²=1 000 000
е)(914+586)²=1500²=2 250 000
ж) (257-143)·(257+143)=114·400=45 600
з)(167-67)·(167+67)=100·234=23 400
и)(162-161)·(162+161):323=1·323:323=1
к)(132-131)(132+131):265=1
л)584+583²-584²+583=
=584+(583²+583)-584²=
=584+583·(583+1)-584²=
=584+583·584-584²=
=584·(1+583-584)=
=584·0=0
м)675+674²-675²+674=675+674²+674-675²=
=675+674·(674+1)-675²=
=675+674·675-675²=
=675·(1+674-675)=
=675·0=0
В решении.
Объяснение:
2. Найдите периметр фигуры. ответ запишите в виде многочлена стандартного вида и укажите его степень.
Памятка:
Как найти сумму и разность многочленов и записать результат как многочлен стандартного вида.
1) Записать многочлены в одну строку, второй многочлен в скобках, между ними знак + или -.
2) Раскрыть скобки. Если между многочленами знак +, во втором многочлене знаки не меняются, если перед скобками знак -, меняются на противоположные.
3) Привести подобные члены.
4) Записать результат в стандартном виде, т.е., в порядке убывания степеней и в алфавитном порядке.
Так как при нахождении периметра выполняется сложение многочленов, можно сразу записать сумму, без скобок.
ху² + 5 + 4ху - 3ху² + 2х² + 4ху =
= -2ху² + 2х² + 8ху + 5.
Степенью многочлена называется наибольшая из степеней его слагаемых.
Степень многочлена (ху²) = 3.