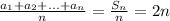
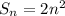
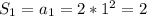
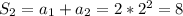
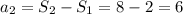
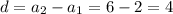
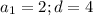
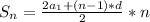
Дано функцію f(x) = (x^2-8x)/(x+1)
Знаходимо найбільше і найменше значення даної функції на проміжку [-5,-2].
f(-5) = ((-5)^2-8*(-5))/(-5+1) = 65/(-4) = -16,25.
f(-2) = ((-2)^2-8*(-2))/(-2+1) = 20/(-1) = -20.
Визначаємо точки екстремуму даної функції.
Знаходимо первісну:
f'(x) = (2x-8)*(x+1) - 1*(x^2-8x))/((x+1)^2) = (x^2 + 2x - 8)/((x + 1)^2).
Прирівнюємо їі до 0 (достатьно чисельник):
x^2 + 2x - 8 = 0, Д = 4+4*8 = 36, х1 = (-2 - 6)/2 = -4, х2 = (-2 + 6)/2 = 2.
Знаходимо знаки первісної:
х = -5 -4 1 2 3
y' = 0,4375 0 -1,25 0 0,4375 .
У точці х = -4 маємо максимум функції,
f(-4) = ((-4)^2-8*(-4))/(-4+1) = 48/(-3) = -16.
Відповідь:
- найбільше значення даної функції на проміжку [-5,-2] дорівнює -16,
- найменше значення даної функції на проміжку [-5,-2] дорівнює -20,
- максимум функції у точці х = -4,
- мінімум функції у точці х = 2.
I день - 0,3 ц
II день - 0,3 ц остатка после I дня
III день - 10,78 ц
Было - ?
предположим, что было х ц зерна, следовательно в первый день смололи (х-0,3х) или 0,7х ц зерна, тогда во второй день (х-0,3х)·0,3 или (0,7х·0,3) ц зерна, а в третий день смололи 10,78 ц зерна
согласно этим данным составляем уравнение:
0,7х-0,7х·0,3=10,78
0,7х-0,21х=10,78
0,49х=10,78
х=10,78:0,49
х=22
х-0.3х-0.7х*0.3=10.78
0.49х=10.78
х=22 (ц) - зерна было.
1) 1-0,3=0,7 (ц) - зерна осталось на мельнице после первого дня.
2) 0,7·0,3=0,21 (ц) - зерна смололи во второй день.
3) 0,7-0,21=0,49 (ц) - смололи в третий день.
4) 10,78:0,49=22 (ц) - зерна смололи за 3 дня.
ответ: 22 центнера зерна смололи на мельнице за три дня.