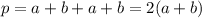
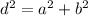
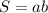
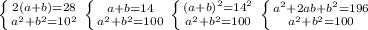
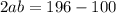
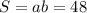
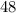
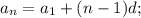

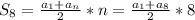
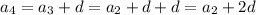
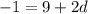
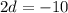

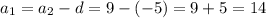
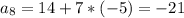
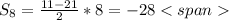
 третьей четверти, в третьей четверти синус отрицательный, по этому из
третьей четверти, в третьей четверти синус отрицательный, по этому из  мы имеем, что
мы имеем, что 
Пусть X первый кусок, а Y второй кусок. Тогда после продажи получилось так: первый кусок= X-Y; а второй кусок=Y-0.5*X;
Составим систему (не знаю как нарисовать её, так что образно):
{ X-Y-10=Y-0.5*X; { 1,5X-2Y=10; | *7 { 10,5X-14Y=70;
{ 1,4(X+Y)=91; <=> { 1,4X+1,4Y=91; | *10 <=> { 14X+14Y=910;
{ 24,5X=980; { X=40; { X=40;
{ 1,4X+1,4Y=91; { 1,4Y=35; { Y=25;
ответ: первая ткань 40м, вторая 25м.
Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке, то есть:
Предварительно вычисляем производную функции первого порядка.
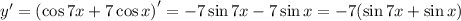
Производная функции в точке 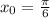
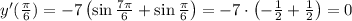
То есть, угловой коэффициент равен 0. Тогда для нахождения значения х, при каждом из которых касательная к данной функции в точках с абсциссой х параллельна касательной в точке 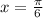 , нужно решить следующее уравнение:
, нужно решить следующее уравнение:
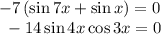
Произведение равно нулю, если хотя бы один из множителей равен 0.
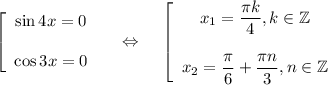
a, b
a²+b²=10²
P=2(a+b)=28
a+b=28:2
a+b=14
a=14-b
(14-b)²+b²=100
196-28b+2b²=100
2b²-28b+96=0
b²-14b+48=0
D=14²-4*48=196-192=4=2²
b₁=(14-2)/2=6 a₁=14-6=8
b₂=(14+2)/2=8 a₂=14-8=6
S=a*b=6*8=48 см²
a₄=a₂+2d
-1=9+2d
2d=-10
d=-5
a₁=a₂-d
a₁=9-(-5)=14
S₈=((2a₁+d(n-1))/2*n=((2*14+(-5)*(8-1))/2*8=(28-35)/2*8=-7/2*8=-28
sina=-√(1-(12/13)²)=-√(25/169)=-5/13
2√3cos300-√12sin135=2√3cos(2π-60)-2√3sin(π/2+45)=2√3cos60-2√3cos45=2√3/2-2√3*√2/2=√3-√6