Пусть сторона квадрата х см, тогда длина прямоугольника (3х) см, а ширина прямоугольника - (х - 5) см.
Т.к. площадь квадрата находят по формуле S = а², где а - сторона квадрата, о площадь данного квадрата равна (х²) см².
А т.к площадь прямоугольника находят по формуле S = a · b, где a и b - длина и ширина прямоугольника, то площадь данного прямоугольника будет равна S = 3х · (х - 5) = 3х² - 15х (см²).
Т.к. площадь квадрата на 50 см² меньше площади прямоугольника, то составим и решим уравнение:
3x² - 15х = x² + 50,
3x² - x² - 15x - 50 = 0,
2x² - 15x - 50 = 0,
D = (-15)² - 4 · 2 · (-50) = 225 + 400 = 625 ; √625 = 25,
x₁ = (15 + 25)/(2 · 2) = 40/4 = 10,
x₂ = (15 - 25)/(2 · 2) = -10·/4 = -2,5 - не подходит по условию задачи.
Значит, сторона квадрата равна 10 см.
ответ: 10 см.
Данное двойное неравенство равносильно системе двух квадратных неравенств:
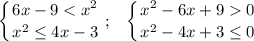
Первое неравенство  .
.
Заметим, что в левой части скрывается квадрат разности (формула  ):
): 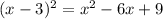 .
.
Неравенство принимает следующий вид: 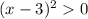 .
.
Так как квадрат числа всегда неотрицательный, то нам не подходит всего лишь один случай: 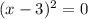 и
и 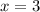 .
.
Значит, первой неравенство эквивалентно тому, что 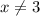 .
.
Второе неравенство 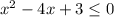 .
.
Вс уравнение 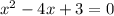 имеет по теореме Виета (утверждающей, что
имеет по теореме Виета (утверждающей, что 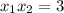 и
и 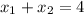 ) корни
) корни 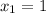 и
и 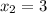 .
.
Из этого следует разложение левой части на множители: 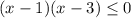 .
.
Метод интервалов подсказывает решение ![x \in [ 1; 3 ]](/tpl/images/1227/3957/60bcc.png) .
.
+ + + - - - + + +
_________![[ \; 1 \; ]](/tpl/images/1227/3957/d73a9.png) _________
_________![[ \; 3 \; ]](/tpl/images/1227/3957/abab5.png) _________
_________
\\\\\\\\\\\\\\\\\\\\\
Значит, второе неравенство равносильно тому, что  .
.
Имеем значительно более простую систему неравенств:

Вполне понятно, что ее решением является 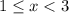 (как пересечения двух промежутков).
(как пересечения двух промежутков).
Или же 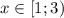 .
.
Задача решена!
ответ: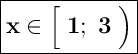
на фото................