По формулам приведения:
если в тригонометрической формуле встречается выражение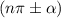
, где 
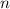— целое число, то вид тригонометрической функции не меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например, 
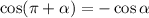(минус, потому что общий угол будет находиться в третьей четверти).если в тригонометрической формуле встречается выражение 
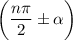, где 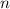— целое число, то вид тригонометрической функции меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например, 
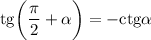(минус, потому что общий угол будет находиться во второй четверти).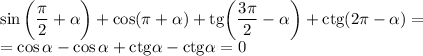
=(a+b)(a²-2ab+b²)=(a+b)(a-b)(a-b)=(a+b)(a-b)²
2)x³-y³-3xy(x-y)=(x-y)(x²+xy+y²)-3xy(x-y)=(x-y)(x²+xy+y²-3xy)=
=(x-y)(x²-2xy+y²)=(x-y)(x-y)(x-y)=(x-y)³