Действительных корней нет.
Комплексные корни:
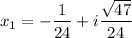
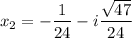
Объяснение:
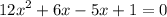
Приводим подобные слагаемые:
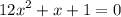
Это обычное квадратное уравнение. Решим через дискриминант.
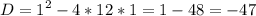
Дискриминант меньше нуля, следовательно действительных корней нет.
Найдем комплексные корни.
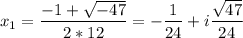
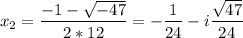
Теория:
Стандартный вид квадратного уравнения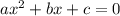 
, 
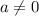
Дискриминант 
Если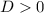 
, то квадратное уравнение имеет два действительных корня.
Если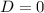 
, то квадратное уравнение имеет один действительных корень.
Если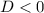 
, то квадратное уравнение не имеет действительных корней, однако комплексные корни существуют.
Комплексное число - число вида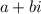 
, где 
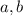- действительные числа, 
- мнимая единица.
Мнимая единица - число, для которого выполняется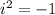 
ответ: потому что уравнение x²-5*x+36 не имеет действительных корней.
Объяснение:
Если уравнение a*x²+b*x+c=0 имеет действительные корни x1 и x2, то a*x²+b*x+c=a*(x-x1)*(x-x2), то есть в этом случае квадратный трёхчлен a*x²+b*x+c можно представить в виде произведения двух многочленов первой степени x-x1 и x-x2. В нашем же случае уравнение x²-5*x+36=0 имеет отрицательный дискриминант D=(-5)²-4*1*36=-119, поэтому это уравнение не имеет действительных корней. А значит, данный квадратный трёхчлен нельзя представить в виде произведения многочленов первой степени.
Из основного тригонометрического тождества
ответ : 5