Находим частные производные:
∂z/∂x=6y-18x+4
∂z/∂y=6x-18y+4
Находим стационарные точки:
{∂z/∂x=0 ⇒ 6y-18x+4=0
{∂z/∂y=0 ⇒ 6x-18y+4 =0
Решаем систему:
{ 6y-18x+4=0 ( умножаем на 3)
{6x-18y+4 =0
{ 18y-54x+12=0
{6x-18y+4 =0
cкладываем
-48х+16=0
х=1/3
y=1/3
Стационарная точка (1/3;1/3) принадлежит области ( см. рис)
Находим вторые частные производные
∂²z/∂x²=-18
∂²z/∂y²=-18
∂²z/∂x∂y=6
A=-18; B=-18: C =6
Δ=AB-C²=(-18)·(-18) -6²>0
A < 0
(1/3;1/3) - точка максимума
z(1/3;1/3)=6·(1/3)·(1/3)-9·(1/3)²-9·(1/3)²+4·(1/3)+4·(1/3)=(2/3)-1-1+(8/3)=4/3 - наибольшее значение функции
На границе
При x=0
z=-9y²+4y
Квадратичная функция при 0 ≤y ≤2
z`=-18y+4
z`=0
y=4/18=2/9 - точка максимума
z(2/9)=-9·(2/9)²+4·(2/9)=(-4/9)+(8/9)=4/9 < 4/3
z(0)=0
z(2)=-9·2²+4·2=-28
При y=0
z=-9x²+4x
Квадратичная функция при 0 ≤x ≤1
z`=-18y+4
z`=0
y=4/18=2/9 - точка максимума
z(2/9)=-9·(2/9)²+4·(2/9)=(-4/9)+(8/9)=4/9 < 4/3
z(0)=0
z(1)=-9·1²+4·1=-5 > -28
При х=1
z=6y-9-9y²+4+4y, исследуем на [0;2], 0 ≤y≤2
z(y)=-9y²+10y-5 - квадратичная функция
z`=-18y+10
z`=0
-18y+10=0
y=10/18=5/9 - точка максимума
при y=5/9
z=-9·(5/9)²+10·(5/9)-5 =- (25/9)+(50/9) -5 =-20/9
Находим значения на концах
z(0)=-5
z(2)=-9·2²+10·2-5=-21 > -28
При y=2
z=12x-9x²-9·2²+4x+4·2, исследуем на [0;1], 0 ≤x≤1
z(y)=-9x²+16x-28 - квадратичная функция
z`=-18x+16
z`=0
-18x+16=0
x=16/18=8/9 - точка максимума
при x=8/9
z=-9·(8/9)²+16·(8/9)-28 =- (64/9)+(128/9) -28 >-28
Находим значения на концах
z(0)=-28
z(1)=-9·1²+16·1-28=-21 > -28
z(1/3;1/3)=4/3 - наибольшее значение функции в области
z(1;2) =-28 - наибольшее значение функции в области
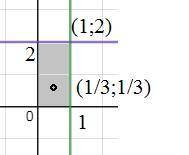
рівняння не має розв'язків
Объяснение:
5х²+8/х²-16 - 2х-1/х+4 + 3х-1/4-х, х≠-4, х≠4
5х²+8/х²-16 - 2х-1/х+4 + 3х-1/4-х=0
5х²+8/(х-4)(х+4)- 2х-1/х+4 +3х-1/-(х-4)=0
5х²+8/(х-4)(х+4) - 2х-1/х+4 - 3х-1/х-4=0
5х²+8-(х-4)(2х-1)-(х+4)(3х-1)/ (х-4)(х+4)=0
5х²+8-(2х²-х-8х+4)-(3х²-х+12х-4)/ (х-4)(х+4)=0
5х²+8-(2х²-9х+4)-(3х²+11х-4)/ (х-4)(х+4)=0
5х²+8-2х²+9х-4-3х²-11х+4/ (х-4)(х+4)=0
5х²+8-2х²+9х-3х²-11х/ (х-4)(х+4)=0
0+8+9х-11х/ (х-4)(х+4)=0
0+8-2х/ (х-4)(х+4)=0
8-2х/ (х-4)(х+4)=0
-2х+8/ (х-4)(х+4)=0
-2(х-4)/ (х-4)(х+4)=0
-2/ х+4=0
- 2/ х+4=0
2/ х+4=0
2=0
рівняння не має розв'язків
1)(4-3х)²=16-24х+9х²
(5х-0,2)²=25х²-2х+0,04
(х-8)(х+8)=х²-64
(3а+5с²)(5с²-3а)=25с4-9а²
2)64-х²=(8-х)(8+х)
25у²-20ху+4х²=(2х-5у)²
3)(х-3)²-(х-1)(х-4)+(х-2)(х+2)=х²-6х+9-х²+4х+х-4+х²-4=х²-х+1
4) 0,49у14-900х8=(0,7у7-30х4)(0,7у7+30х4)
(х-7)²-100=(х-7-10)(х-7+10)=(х-17)(х+3)
8у³-а³=(2у-а)(4у²+2ау+а²)