Первый
(1,8 - 0,3y) * (2y + 9) = 0
(1,8 - 0,3y) = 0 (2y + 9) = 0
-0,3y = - 1,8 2y = -9
y = -1,8 : (-0,3) y = (-9) : 2
y = 6 y = -4,5
ответ: y₁ = -4,5; y₂ = 6.
Второй
(1,8 - 0,3y) * (2y + 9) = 0
3,6y + 16,2 - 0,6y² - 2,7y = 0
-0,6y² + 0,9y + 16,2 = 0
a = -0,6; b = 0,9; c = 16,2
D = b² - 4ac = 0,9² - 4 * (-0,6) * 16,2 = 0,81 + 38,88 = 39,69
Так как дискриминант больше нуля (D = 39,69), то уравнение имеет два корня:
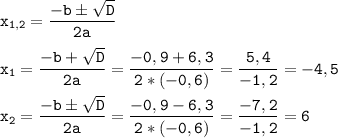
ответ: y₁ = -4,5; y₂ = 6.
f'(x)=-3*x²+3*1 ⇒ f'=0⇒3-3*x²=0⇒3*x²=3⇒x=1 для заданного промежутка от 0 до 4. Это точка max так как производная меняет знак с + (при х=0 производная равна 3) на минус (при х=2 производная равна -12+3=-9). Максимум функции равен ymax=-1³+3*1*|1-3|=-1+3*2=5
При х=0 имеем y=0
При х=4 имеем y=-4³+3*4*|4-3|=-52 - точка минимума.