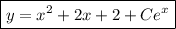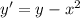
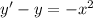
Первый
Решение ищем как сумму общего решения однородного уравнения, соответствующего данному неоднородному, и частного решения данного неоднородного уравнения.
Составим однородное уравнение, соответствующее данному неоднородному:
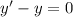
Решаем уравнение с разделяющимися переменными:
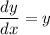
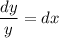
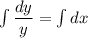
Общее решение однородного уравнения:
Частное решение ищем в виде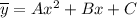 
.
Найдем производную:
Подставим в уравнение:
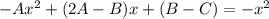
Условие равенства левой и правой частей:
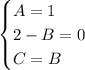
Частное решение неоднородного уравнения:
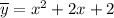
Искомое решение:
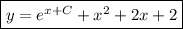
Второй
Решение ищем в виде произведения двух ненулевых функций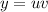 
. Тогда 
.
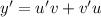Пусть сумма первого и третьего слагаемого в левой части равна нулю:
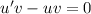
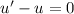
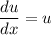
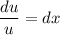
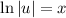
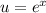
Тогда второе слагаемое в левой части равно правой части:
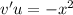
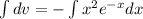
Интеграл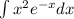 
вычислим отдельно. Будем использовать интегрирование по частям: 
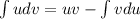(не записывая произвольную константу):
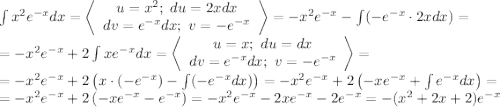
Таким образом:
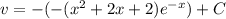
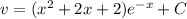
Искомая функция:
