x² + 2x + 3 = ( x+1)² + 2 > 0 для всех х ⇒ | x² + 2x + 3 | = x² + 2x + 3
x² + 2x + 3 -3x -45 = 0 ⇔ x² -x - 42 = 0 ⇔ x = 7 или х = -6 ( по
теореме , обратной к теореме Виета )
ответ : х = 7 или х = -6
км/ч. 
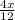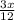км/ч, что на 20 км больше. - = 20
- 
= 20
=20
y=x^2-6x+5
Находим корни по Виету. сумма корней равна 6, произведение 5. Это 1 и 5. Значит y=x^2-6x+5=(х-1)(х-5). Значит парабола пересекается с осью х в точках 1 и 5. Вершина параболы будет в точке с координатами (1+5)/2=3. Наименьшее значение функции будет тоже в точке с такой координатой по х, т.к. парабола смотрит веточками вверх. При х=3 координата по у равна -4. (х=3 подставь в уравнение). Значит наименьшее значение функции -4.
График функции - парабола ветками вверх с вершиной в точке (3;-4), пересекается с осью абсцисс в точках 1 и 5 по х, с осью ординат - в точке 5
