Пусть х км/ч - скорость автобуса, тогда (80 - х) км/ч - скорость сближения при движении вдогонку; 20 мин = 20/60 ч = 1/3 ч; 1/3х км - проедет автобус за 20 мин (расстояние между автобусом и автомобилем). Уравнение:
1/3х : (80 - х) = 1
1/3х = 1 · (80 - х)
1/3х = 80 - х
1/3х + х = 80
4/3х = 80
х = 80 : 4/3
х = 80 · 3/4
х = 20 · 3
х = 60
ответ: 60 км/ч.
Проверка:
1) 60 · 1/3 = 60/3 = 20 км - проедет автобус за 20 минут;
2) 80 - 60 = 20 км/ч - скорость сближения при движении вдогонку;
3) 20 : 20 = 1 ч - время движения до встречи.
x = 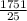 или 70,04
или 70,04
Объяснение:
Сначала найдем ОДЗ: x > 0.
Потом переместим с иксом в левую часть, а с постоянной в правую:
- log5 (x) = -log5 (17) - log5 (4,12).
Вынесем знак минуса за скобки: -log5 (x) = -(log5 (17) + log5 (4,12)).
Вычислим сумму логарифмов: -log5 (x) = -log5 (70,04).
Изменим знаки обеих частей уравнения: log5 (x) = log5 (70,04).
Преобразуем десятичную дробь в обыкновенную: log5 (x) = log5 (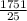 ).
).
Поскольку основания логарифмов одинаковые, приравняем их аргументы: x = 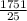 , при этом x > 0.
, при этом x > 0.
Раз х и правда больше нуля, значит x = 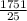 .
.
Но раз в ответ надо что-то маленькое в окошко, тогда переводим в десятичную дробь --> 70,04.