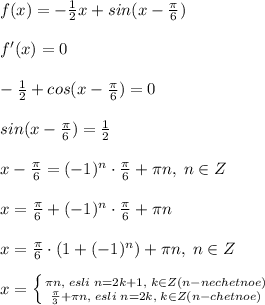
Объяснение:
1. а) необходимо на место х в дроби подставить заданные значения, т.е.:
при х = 0: (х+3)/(1-4х) = (0+3)/(1-0*4) = 3
при х = -1: (-1+3)/(1-4*(-1)) = 2/5 или же 0,4 это одно и то же
при х = 0,3: (0,3+3)/(1-0,3*4) = 3,3 / (-0,2) = -33/2 = -16,5
при х = -1/4: (-1/4+3)/(1-(-1/4)*4) = (-11/4) / 2 = -11/8
при х = 7: (7+3)/(1-4*7) = 10 / (-27) = - 10/27
при х = 3/2: (3/2+3)/(1-4*(3/2)) = (9/2) / (-5) = -9/10
б) дробь равна нулю, если числитель равен нулю, т.е.:
х + 3 = 0, при х = -3
в) дробь не имеет смысла, если знаменатель равен нулю, что вполне логично, т.к. на 0 делить нельзя, по крайней мере в школе
1 - 4х = 0, х = 1/4
2. а) нужно просто подставить х = -1 и у = 1:
((-1 - 3)^2 + 1^2 -2) / ((2*1 - (-1))*(5 + (-1)^4)) = ((-4)^2 + 1 - 2) / ((2 + 1)*(5 + 1)) = 15 / 18 = 5/6; вычисления в этом пункте лучше еще раз перепроверить
б) здесь можно приравнять скобку в знаменателе к 0:
(2у - х) = 0, при х = 0 и у = 0