Всего три пары - 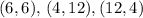
Объяснение:
Для того чтобы решить задачу, нужно правильно сформулировать проблему -
"Требуется найти все пары 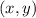 , где
, где 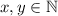 так что
так что 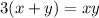 ."
."
Из равенства 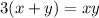 очевидно что
очевидно что 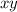 делится на 3. Следовательно хотя бы одно из чисел
делится на 3. Следовательно хотя бы одно из чисел 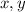 делится на 3. Без огранчения общности, предположим что
делится на 3. Без огранчения общности, предположим что 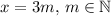 .
.
Следовательно, высшеупомянотое равенство преообразовывается в
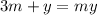 , из которого выводим
, из которого выводим 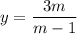 .
.
Заметим что отсюда выходит что, 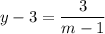 .
.
Т.к. 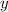 цело только и только тогда, когда
цело только и только тогда, когда 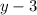 цело, то следовательно, 3 должно делится на
цело, то следовательно, 3 должно делится на  .
.
Число 3 делится только на четыре числа - 3, -3, 1, -1. Но лишь только два из них подходят - 3 и 1.
Следовательно,
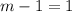 или
или 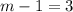 .
.
Т.е.,
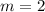 или
или 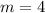
Отсюда получаем две пары - 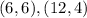 . Однако очевидно, что также и пара
. Однако очевидно, что также и пара 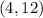 подходит.
подходит.
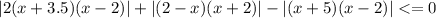
Заметим что если |2x^2+3x-14| будет больше нуля, тогда минимум функции будет достигаться в случае когда все модули раскроются с знаком+:
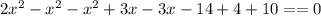
То-есть при |2x^2+3x-14|>0 минимальное значение 0.
при |2x^2+3x-14|<0 минимальное значение будет достигаться когда все модули раскроются с знаком-.
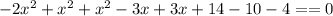
То-есть как бы не раскрылись модули минимальное значение функции будет 0.
-----------------
Осталось только найти такие промежутки при которых:
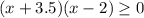
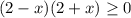
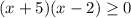
И
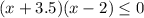
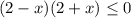
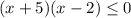
Решив эту систему уравнений методом интервалов мы получаем ответ:
x∈[-3.5;-2]∪{2}
ответ будет такой
1)7+13= 20
2)100% /20=5
3) 13*5=65%
65% изюма .