У драконов по 3 головы, значит число (26 - (головы сороконожек) ) должно быть кратным 3.
Максимум сороконожек могло быть: 298 \ 40 = 7 (штук) , смотрим:
26 - 7 = 19 (не кратно 3)
26 - 6 = 20 (не кратно 3)
26 - 5 = 21 (кратно 3)
26 - 4 = 22 (не кратно 3)
26 - 3 = 23 (не кратно 3)
26 - 2 = 24 (кратно 3)
26 - 1 = 25 (не кратно 3)
26 - 0 = 26 (не кратно 3)
Итак, если сороконожек было 5, то драконов было:
(26 - 5) / 3 = 7
Тогда ног у драконов:
(298 - 5 * 40) / 7 = 14
А если сороконожек было 2, то драконов было:
(26 - 2) / 3 = 8
Тогда ног у драконов:
(298 - 2 * 40) / 8 = 12,25 - этого быть не может.
ответ: У дракона 14 ног.
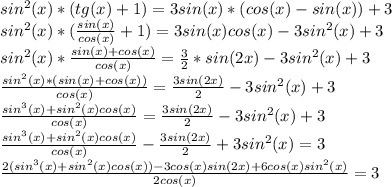
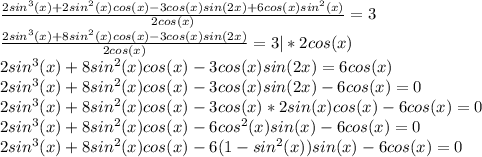
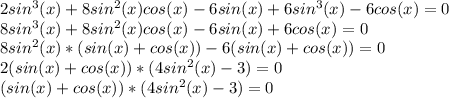
sin(x)+cos(x) = 0 или 4sin²(x)-3 = 0
sin(x) = -cos(x) |:cos(x) 4sin²(x) = 3
tg(x) = -1 sin²(x) = 3/4
x₁ = 3π/4 + πn, n∈Z sin(x) = ±√3/2
sin(x) = -√3/2 или sin(x) = √3/2
x₂ = arcsin(-√3/2) + 2πn x₄ = arcsin(√3/2) + 2πn
x₃ = π-arcsin(-√3/2) + 2πn x₅ = π-arcsin(√3/2) + 2πn
x₂ = -π/3 + 2πn x₄ = π/3 + 2πn
x₃ = π+π/3 + 2πn x₅ = π-π/3 + 2πn
x₂ = 5π/3 + 2πn, n∈Z x₄ = π/3 + 2πn, n∈Z
x₃ = 4π/3 + 2πn, n∈Z x₅ = 2π/3 + 2πn, n∈Z
Следовательно:
x₄ = π/3 + 2πn, n∈Z,
x₅ = 2π/3 + 2πn, n∈Z
ответ: x₁ = 3π/4 + πn, n∈Z;
x₄ = π/3 + 2πn, n∈Z;
x₅ = 2π/3 + 2πn, n∈Z
D=4+12=16
График - вогнутая парабола, схеметично начертив увидим, что решение неравентсва = x ⊂ (-∞; -1]∪[3; ∞)
Составим систему, раскрыв модуль со знаками (+) и (-):
Решим уравнения отдельно.
1)
2)
x(x-3)=0
ответ: -2; 3.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Найдём точки зануления модулей.
Этими тремя точками разобьём числовую прямую на 4 интервала и решим уравнение в каждом из них:
I II III IV
--------(1)--------(2)--------(3)--------
I) Раскроем модули на первом интервале (-∞; 1]: если положителен, то со знаком «+», если отрицателен, то «-»:
(1-x)+(2-x)=(3-x)+4
X=-4 => подходит, т.к. лежит в рассматриваемом интервале.
II) Раскроем модули на интервале [1; 2]:
(x-1)+(2-x)=(3-x)+4
X=6 => не подходит, так не принадлежит текущему интервалу [1; 2].
III) Раскроем модули на интервале [2; 3]:
(x-1)+(x-2)=(3-x)+4
IV) Раскроем модули на интервале [3; ∞):
(x-1)+(x-2)=(x-3)+4
X=4 => подходит.
ответ: -4; 4.