Відповідь:
1.
f(2)=8
f(-1)= - 2,5
нулі: f(0)=0
2. D(f): x ∈ (-∞;4)∪(4;6)∪(6;+∞)
3) в завданні
5)х ∈ [-5;-4) ∪(-4;4) ∪(4;+∞)
6)p=8 q=22
Пояснення:
1)f(2)=1/2*2²+3*2=2+6=8;
f(-1)=1/2*(-1)²+3*(-1)=0,5-3=-2,5
нулі х=0; f(0)=1/2*0+3*0=0 (при у=0 х=0)
2.область визначення функції: оскільки це дріб, то знаменник не може бути рівний 0
х²-10х+24≠0 D=(-10)²-4*1*24=100-96=4
x₁≠(10-2)/2≠4
x²≠(10+2)/2=6
Відповідь: D(f): x ∈ (-∞;4)∪(4;6)∪(6;+∞)
3. Побудувати графік функції:
це парабола , вітки направлені догори
Знайдемо точки перетину з вісью ОХ
x²+2x-3=0 по теоремі Вієта х1= - 3 , x2= 1.
координати вершини: хв=-2/2=-1, ув=(-1)²+2*(-1)-3=-4 (-1;-4)
при х=0, у=-3
графік перемалюєш з картинки
1)f(x)>0 при х ∈ (-∞; -3) ∪ (1;+∞)
f(x)<0 при х ∈ (-3; 1)
2)Е(f) : y ∈ (-5;+∞)
3) функція зростає при х ∈ [-1; +∞)
4.
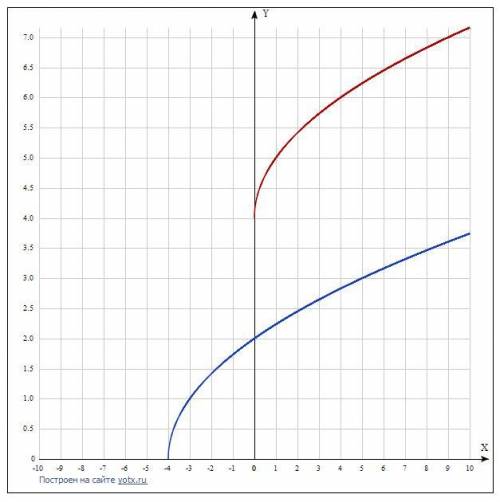
маєш в файлі синя- перша, червона -друга( побудуй функцію онлайн і перемалюй таблицю точок)
5. Область визначення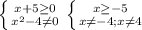
Відповідь: ОДЗ: х ∈ [-5;-4) ∪(-4;4) ∪(4;+∞).
6) хв=-4 ; -4=-p/2*1;p=8
ув=6
6=(-4)²+8(-4)+q;
q=6-16+32=22
f(x)=x²+8x+22
p=8 q=22
In(x)/x²→∞, в то время x→0 слева, а
In(x)/x²→-∞, в то время как x→0 справа, следовательно, x=0- вертикальная асимптота.
x=0
Не принимая во внимание логарифм, рассмотрим рациональную функцию
R(x) = axⁿ/bx^m, где n- степень числителя, а m степень знаменателя.
1. если n<m, то ось x, y=0, является горизонтальной асимптотой.
2. если n=m, то горизонтальной асимптотой является прямая y= a/b
Если n>m , то не существует горизонтальной асимптоты (только наклонная асимптота).
Найдем m и n
n=0
m=2
Поскольку n<m, ось X, y=0
, является горизонтальной асимптотой.
y=0
Для логарифмических и тригонометрических функций не существует наклонных асимптот.
Нет наклонных асимптот
Это множество всех асимптот.
Вертикальные асимптоты: x=0
Горизонтальные асимптоты: y=0
Длина маршрута - 270 км.
х + 1,2х + 0,8х = 270
3х = 270
х = 90
90 км - путь в первый день.