Question

Возьмём простейшее уравнение sin x = 1. его корень таков: x=π/2+2πk, k€z (это так называемый частный случай). теперь решим это же уравнение, воспользовавшись общей формулой корней синуса. получим после использования данной формулы следующий корень: x=(-1)^n×arcsin(1)+πk => (-1)^n×π/2+πk.
мой, собственно, вопрос: куда из корня уравнения частного случая делась (-1)^n и откуда в нём появилась двойка перед πk, ведь в общей формуле её нет? объясните, , связь между частным случаем корня и общим (если она существует,

Answer 1

Объяснение:

Конечно же обе формулы дают ОДНИ И ТЕ ЖЕ решения. Просто запись в частном случае более лёгкая для восприятия.

$sinx=1\; \; \Rightarrow \; \; x=\frac{\pi}{2}+2\pi k\; ,\; k\in Z$

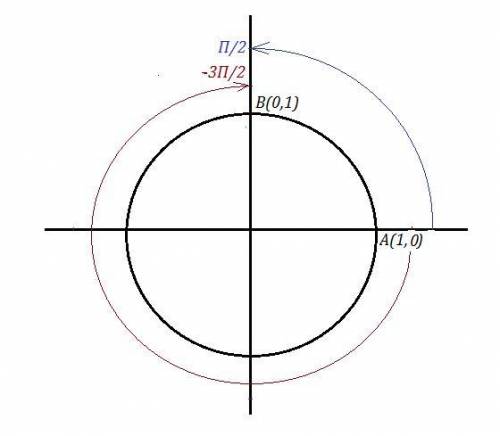
Из этой формулы следует, что sinx=1  при х=П/2 , причём, если эту точку повернуть на один круг (+/-2П), два круга (+/-4П), три круга (+/-6П)  и так далее, то придём в одну ту же точку В на тригонометрическом круге с декартовыми координатами (0,1) . Смотри рисунок. Поворачивать точку можно против часовой стрелки (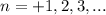 $n=+1,2,3,...$ ) или по часовой стрелкe ($n=-1,-2,-3,...$ ) .

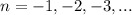В случае общей формулы надо рассматривать чётные и нечётные значения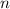  $n$ .

Если k- чётно, то получаем

$k=2n\, :\; \; x=(-1)^{2n}\cdot arcsin1+\pi \cdot 2n=+1\cdot \frac{\pi}2}+2\pi n,\; n\in Z$

То есть получили ту же формулу, что и в частном случае.

Если k - нечётно, то получаем

$k=2n-1\, :\; \; x=(-1)^{2n-1}\cdot arcsin1+\pi \cdot (2n-1)=-1\cdot \frac{\pi}{2}+\pi \cdot (2n-1)=\\\\=-\frac{\pi}{2}+2\pi n-\pi =-\frac{3\pi }{2}+2\pi n \; ,\; n\in Z$

На вид эта формула не похожа на частный случай, но точка х= -3П/2  получается из точки с дек. координатами А(1,0) путём её поворота на 270° (3П/2) по часовой стрелке (отрицательное направление поворота, поэтому знак (-) пишем ). И попадёт она в точку В(0,1). Но ведь мы попадём в точку В(0,1)  и при повороте точки А(1,0) против часовой стрелки ( положительное направление поворота) на 90° (П/2) .

Поэтому запись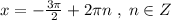  $x=-\frac{3\pi}{2}+2\pi n\; ,\; n\in Z$  равноценна записи  $x=\frac{\pi}{2}+2\pi n\; ,\; n\in Z$ .

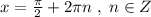Конечно, предпочтительнее сразу писать частный вид формулы для решения уравнения  sinx=1, потому что он более простой в записи , но описывает те же решения, что и частный случай.

Answer 2

Объяснение:

Смотри, значит. При нечетных n получим, что первое слагаемое отрицательно, т. е. находится на оси sin(x) между III и IV четвертями. Прибавляя нечетное число π, получаем точку сверху, как раз ту, которая является решением.

Теперь возьмем n четное. Первое слагаемое положительно, а так же получаем некоторое четное количество оборотов (четное число π), которое возвращает нас в эту же точку, так как является периодом функции sin(x)