Теплохід пройшов 100 км за течією річки і 64 км проти течії , витративши на це 9 год. Знайдіть власну швидкість теплохода , якщо власна швидкість течії дорівнює 2 км/ год
- - - - - - - - - -
Теплоход км по течению реки и 64 км против течения, затратив на это 9 ч. Найдите собственную скорость теплохода, если скорость течения равна 2 км/ч
скорость теплохода → x км/ч
скорость теплохода по течению реки будет (x+2) км/ч
скорость теплохода против течению реки будет (x -2) км/ч
составим уравнение
100 / (x+2) +64 /( x- 2) = 9 ; x > 2 км/ч
100 (x- 2)+ 64( x+2) =9 (x+2) (x -2) ;
100x- 200 + 64x+128 =9 (x²- 2²) ;
164x -72 =9x² - 36 ;
9x² - 164x + 36 =0 ; D₁= D/4 =82² - 9*36 =6400 = 80²
x =( 82 ±80)/9 =162 /9 =18 (км / ч)
x =( 82 - 80)/9 =2/ 9 ( км / ч) < 2 км / ч не решение
ответ: 18 км / ч.
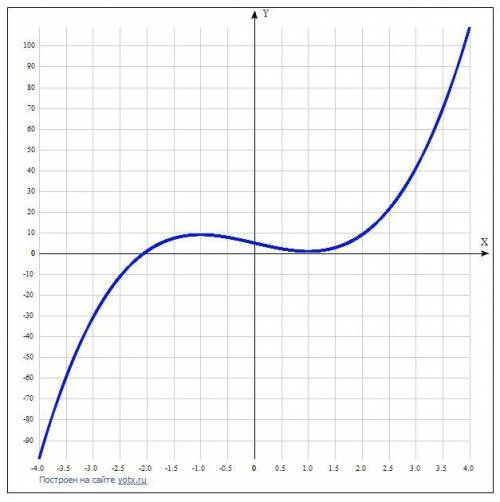
Дана функция у = 2х³ - 6х + 5.
1) Область определения функции - ограничений нет, х ∈ (-∞; +∞).
Точки разрыва функции - нет.
2) Четность или нечетность функции.
y(-x)=-2·x3+6·x+5 ≠ у(х). Функция общего вида
3) Периодичность функции - нет.
4) Точки пересечения кривой с осями координат.
Пересечение с осью 0Y : x=0, y=5
Пересечение с осью 0X
y=0
2·x³-6·x+5=0 . Решается по методу Кардано.
x1=-2.0536232
5) Исследование на экстремум y = 2*x^3-6*x+5.
1. Находим интервалы возрастания и убывания. Первая производная.
f'(x) = 6·x²-6
Находим нули функции. Для этого приравниваем производную к нулю
6·x² - 6 = 0 , 6(x²- 1) = 0.
Откуда: x1 = -1 , x2 = 1.
(-∞ ;-1) (-1; 1) (1; +∞)
f'(x) > 0 f'(x) < 0 f'(x) > 0
функция возрастает функция убывает функция возрастает
В окрестности точки x = -1 производная функции меняет знак с (+) на (-). Следовательно, точка x = -1 - точка максимума. В окрестности точки x = 1 производная функции меняет знак с (-) на (+). Следовательно, точка x = 1 - точка минимума.
2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная f''(x) = 12·x.
Находим корни уравнения. Для этого полученную функцию приравняем к нулю: 12·x = 0.
Откуда точки перегиба:
x1 = 0
(-∞ ;0) (0; +∞)
f''(x) < 0 f''(x) > 0
функция выпукла функция вогнута
6) Асимптоты кривой.
y = 2·x³-6·x+5.
Вертикальные асимптоты – нет.
Горизонтальные асимптоты графика функции:
Горизонтальную асимптоту найдем с предела данной функции при x->+∞ и x->-∞. Соответствующие пределы находим:
• lim x³-6x+5, x->+∞ = ∞, значит, горизонтальной асимптоты справа не существует.
• lim x³-6x+5, x->-∞ = -∞, значит, горизонтальной асимптоты слева не существует.
Наклонные асимптоты графика функции.
Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при x->+∞ и x->-∞. Находим пределы:
• lim x³-6x+5/x, x->+∞ = ∞, значит, наклонной асимптоты справа не существует,
• lim x³-6x+5/x, x->-∞ = ∞, значит, наклонной асимптоты слева не существует.
х=-3
2)х=3-12
х=-9
3)0,2х=8-12
0,2х=4
х=4:0,2
х=20
4)10х-7-32=-16
10х=-16+7+32
10х=23
х=2,3
5)х=2+2
х=4