1) Область определения { x^2 - 1 > 0 { log(1/2) (x^2 - 1) > 0 Функция y = log(1/2) (x) - убывающая, поэтому { (x + 1)(x - 1) > 0 { x^2 - 1 > 1; x^2 - 2 > 0 Получаем { x< -1 U x > 1 { x < -√2 U x > √2 Область: x < -√2 U x > √2 2) Решаем неравенство Функция y = log3 (x) - возрастающая, поэтому log3 (log(1/2) (x^2 - 1)) < 1 = log3 (3) log(1/2) (x^2 - 1) < 3 = log(1/2) (1/8) Функция y = log(1/2) (x) - убывающая, поэтому x^2 - 1 > 1/8 x^2 > 1 + 1/8 = 9/8 |x| > 3/√8 ~ 1,06 < √2 ответ: x < -√2 U x > √2 Неравенство вообще не имеет значения, все определяет область определения, простите за тавтологию.
Площадь треугольника полупроизведение сторон и синус угла между ними S=0,5*a*b*sinx поскольку это равнобедренный треугольник, то стороны а и b одно и тоже плюс нам дан угол и площадь т.е. можно переписать формулу площади уже с известными нам величинами значит боковые стороны равны 12 если в этом треугольнике провести высоту(биссектрису(медиану)), то получится два прямоугольных треугольника с углами 60,30,90 половина основания лежит против угла в 60 градусов, используем синус: поскольку это половинка основания, то все основание будет в два раза больше итоговый ответ: стороны равны
1)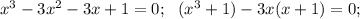
x+1=0 x1 = -1
ответ: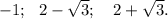
2)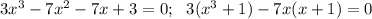
x+1=0, x1 = -1.
ответ: -1; 1/3; 3.