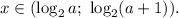№ 2:
при каком значении параметра a уравнение |x^2−2x−3|=a имеет три корня?
введем функцию
y=|x^2−2x−3|
рассмотрим функцию без модуля
y=x^2−2x−3
y=(x−3)(х+1)
при х=3 и х=-1 - у=0
х вершины = 2/2=1
у вершины = 1-2-3=-4
после применения модуля график отражается в верхнюю полуплоскость
при а=0 - 2 корня (нули х=3 и х=-1)
при 0< а< 4 - 4 корня (2 от исходной параболы, 2 от отображенной части)
при а=4 - 3 корня (2 от исходной параболы, 1 от вершины х=1)
при а> 4 - 2 корня (от исходной параболы)
ответ: 4
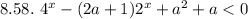
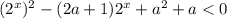
Замена: 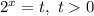
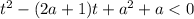
Имеем квадратичную функцию 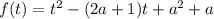 , графиком которой является парабола с ветвями, направленными вверх.
, графиком которой является парабола с ветвями, направленными вверх.
Найдем возможные точки пересечения параболы с осью абсцисс.
Для этого решим квадратное уравнение:
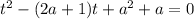
Найдем дискриминант данного уравнения:
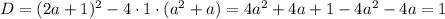
Имеем 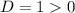 , значит данное уравнение имеет ровно 2 корня:
, значит данное уравнение имеет ровно 2 корня:
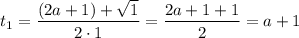
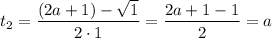
Имеем две точки пересечения параболы с осью абсцисс.
Пусть  . Тогда
. Тогда 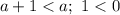 . Имеем неверное неравенство. Следовательно, при всех значениях параметра
. Имеем неверное неравенство. Следовательно, при всех значениях параметра  имеем
имеем 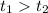 .
.
Тогда квадратичная функция 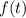 будет меньше 0 при
будет меньше 0 при 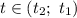
Последнее можно записать так:

Обратная замена:
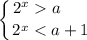
Если 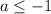 , то имеем:
, то имеем: 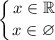
Решением такой системы неравенств является 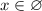
Если 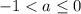 , то имеем:
, то имеем: 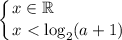
Решением такой системы неравенств является 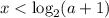
Если 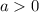 , то имеем:
, то имеем: 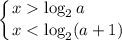
Решением такой системы неравенств является интервал 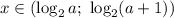
![a \in (-\infty; \ -1]](/tpl/images/1357/0229/00410.png) , то нет корней;если
, то нет корней;если ![a \in (-1; \ 0]](/tpl/images/1357/0229/7e5c2.png) , то
, то 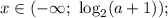 если
если 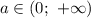 , то
, то