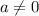. Иначе уже число не двузначное :)). a=1,2,3,4,5,6,7,8,9 - это все возможные числа. b=0,1,2,3,4,5,6,7,8,9. Сумма квадратов цифр равна 
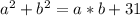- это по условию задачи.
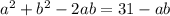
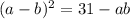
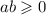, то правая часть меньше или равна 31. Значит надо найти квадраты чисел меньших 31, но больше 0. Задача вполне выполнимая. В порядке убывания 25, 16, 9, 4,1. 0 - на всякий случай. 
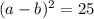. При а=1 и b=6, а также, наоборот, а=6, b=1 получаем, что квадрат разности выполняется. При а=3 и b=2, и наоборот, квадрат разности не выполняется. То есть подходят только пары а=6, b=1 и а=1 и b=6. 
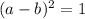. То есть получаем числа 65 и 56. Остальные пары, вроде 2 и 15 недопустимы.
Сумма членов S =((a1 + an)*n)/2.
an = a1 + d(n - 1). Подставим: S =((a1 + a1 + d(n - 1))*n)/2
Отсюда получаем формулу для определения d:
Пятый член равен а5 = -9 + 16*4 = 55.
Теперь рассмотрим неизвестные 5 членов.
Пусть первый из этих пяти равен "х".
Сумма пяти равна: х + (х + 16) + (х + 32) + (х + 48) + (х + 64).
Получаем уравнение: 515 = 5х + 160
откуда х = (515 - 160)/5 = 355/5 = 71.
Зная, что а5 = 55, получаем 55 + 16 = 71, то есть это шестой член.
ответ: число членов этой прогрессии равно 10.