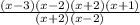сокращаем ,но помним, что x не равен +-2. Получили (x-3)(x+1). график прикрепил, красные точки выколотые y=m -горизонтальная прямая на уровне m. из графика видим, 1 точка будет в вершине и на уровне выколотых точек. ищем y вершины. х вершины по формуле -b/2a, график имеет формулу x^2-2x-3, b=-2, a=1, x вершины=1, подставим 1 в уравнение, получим -4, это у, прим m=-4 1 общая точка. теперь выколотые рассмотрим, подставим в уравнение +-2, получим -3 и 5 соответственно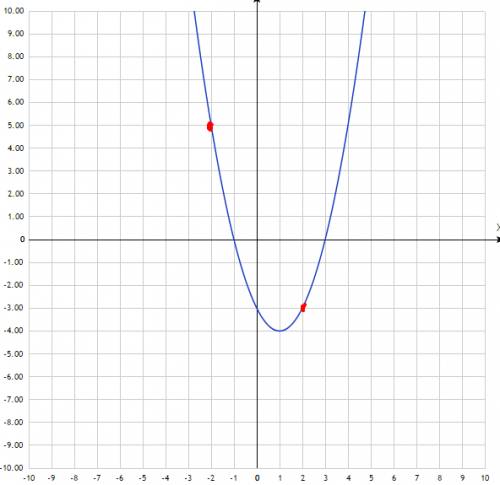
Чтобы найти tg надо найти sin
SinL=√1-(-15/17)^2=√1-225/289=√64/289
=8/17. TgL=sinl/cosl=8/17*(-17/15) при умножении переворачиваем дробь.
ответ: tgL=-8/15
2)0<L<Pi/2 Первая четверть
TgL=3
cosL=√1/1+3^2
cosL=1/√10 и это ответ