20 и 19 марок.
Объяснение:
Пусть на первой странице было x марок, а на второй странице - y марок. После того, как 35% марок с первой страницы переложили на вторую, на первой странице стало x-0,35x=0,65x марок, а на второй странице стало y+0,35x марок. По условию задачи, на второй странице марок стало в 2 раза больше, чем на первой. Тогда
2*0,65x=y+0,35x
1,3x=y+0,35x
1,3x-0,35x=y
0,95x=y
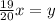
По смыслу задачи, x и y - положительные целые числа. Минимальное положительное целое значение x, при котором y также будет положительным целым, равно 20. Если x=20, 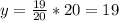 .
.
ответ:
раскроем выражение в уравнении
((xy+x)−3)2+((xy+y)−4)2=0
получаем квадратное уравнение
2x2y2+2x2y+x2+2xy2−14xy−6x+y2−8y+25=0
это уравнение вида
a*x^2 + b*x + c = 0
квадратное уравнение можно решить
с дискриминанта.
корни квадратного уравнения:
x1=d−−√−b2a
x2=−d−−√−b2a
где d = b^2 - 4*a*c - это дискриминант.
т.к.
a=2y2+2y+1
b=2y2−14y−6
c=y2−8y+25
, то
d = b^2 - 4 * a * c =
(-6 - 14*y + 2*y^2)^2 - 4 * (1 + 2*y + 2*y^2) * (25 + y^2 - 8*y) = (-6 - 14*y + 2*y^2)^2 - (4 + 8*y + 8*y^2)*(25 + y^2 - 8*y)
уравнение имеет два корня.
x1 = (-b + sqrt(d)) / (2*a)
x2 = (-b - sqrt(d)) / (2*a)
171 в любой степени будет оканчиваться на один.
Сумма этих двух чисел оканчивается на 1+4=5
Любое число, оканчивающееся на 5, кратно пяти