Объяснение:
1. При пересечении двух прямых секущей, образовавшиеся односторонние углы 1 и 2 в сумме дают 180 градусов. Значит две непересекающиеся прямые - параллельны. Значит, углы 3 и 4 - соответственные и равны друг другу.
ответ: угол 4 равен 55 градусов.
2. Угол AOD и DOB - смежные. Значит AOD=180-108=72 градуса. OK - биссектриса, значит AOK=DOK=72/2=36 градусов.
ответ: DOK=36 градусов.
3. DMC=DMB=60 градусов. CMB=60*2=120. AMC+CMB=180 (смежные углы) AMC=180-120=60 градусов.
ответ: CMA=60 градусов
Пусть при пересечении прямых а и с секущей АВ накрест лежащие углы равны, т.е. угол 1 = углу 2.
Теперь докажем, что а || с.
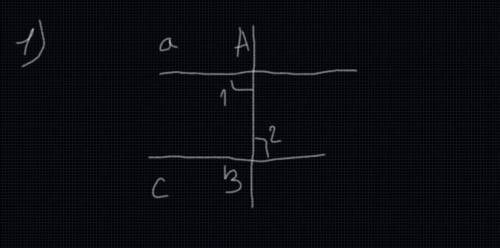
Первый случай: Нам даны 2 прямых угла, которые равны (угол 1 = углу 2). Т.к. углы = 90 градусам, то прямые а и с перпендикулярны к прямой АВ и, получается, а || с. (1 вложение)
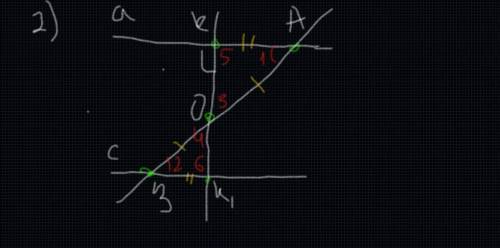
Второй случай: Нам даны 2 не прямых угла, которые равны (угол 1 = углу 2). Тогда проведем из середины О отрезка АВ перпендикуляр ОК к прямой а. На прямой с отложим отрезок ВК1 (ВК1=АК) и проведем отрезок ОК1. Получившиеся треугольники будут равны по первому признаку*, поэтому угол 3 = углу 4, угол 5 = углу 6.
Из равенства угол 3 = углу 4 следует, что точка К1 лежит на продолжении луча ОК, т.е. точки К, О, К1 лежат на одной прямой.
Из равенства угол 5 = углу 6 следует, что угол 6 - прямой (т.к. угол 5 тоже прямой). Следовательно, прямые а и с перпендикулярны к прямой КК1, поэтому а || с. (вложение 2)
ответ: верно утверждение 2
* - первый признак равенства треугольников - если 2 стороны и угол между ними одного треугольника соответственно равны 2м сторонам и углу между ними другого треугольника, то такие треугольники равны.
{x²-4xy+4y²=0⇒(x-2y)²=0⇒x-2y=0⇒x=2y
{x/(x+3)+(x+3)/x=17/4⇒2y/(2y+3)+(2y+3)/2y=17/4
(2y+3)/2y=a
1/a+a=17/4
4a²-17a+4=0
D=289-64=225
a1=(17-15)/8=1/4⇒(2y+3)/2y=1/4
8y+12=2y
6y=-12
y1=-2⇒x1=-4
a2=(17+15)/8=4⇒(2y+3)/2y=4
2y+3=8y
6y=3
y2=0,5⇒x2=1
(-4;-2);(1;0,5)
2
{x²-2xy+y²=0⇒(x-y)²=0⇒x-y=0⇒x=y
{(y+1)/(y+2)+(y+2)/(y+1)=25/12
(y+2)/(y+1)=a
a+1/a=25/12
12a²-25a+12=0
D=625-576=49
a1=(25-7)/24=3/4⇒(y+2)/(y+1)=3/4
4y+8=3y+3
y1=-5⇒x1=-5
a2=(25+7)/24=4/3⇒(y+2)/(y+1)=4/3
3y+6=4y+4
y2=2⇒x2=2
(-5;-5);(2;2)