
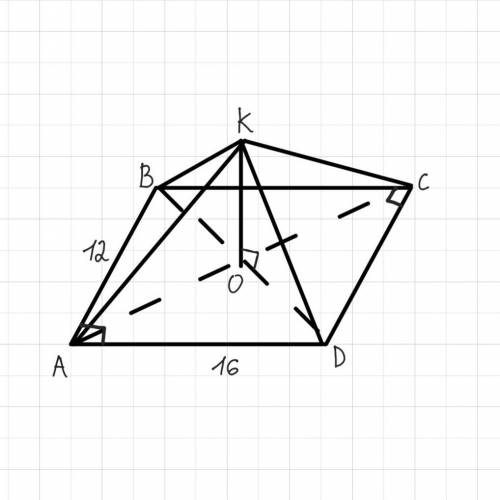
Дано: ABCD - прямоугольник, AB=DC= 12 см, BC=AD=16 см, AC и BD - диагонали ABCD, AC∩BD = т.О, K ∉ ABCD, OK⊥ABCD, КО=5√5 см.
Найти: АК.
Решение.
Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности => точка О - центр описанной около прямоугольника ABCD окружности.
Длины отрезков AO, OC, BO, OD равны между собой и равны радиусу описанной окружности.
AO=OC=BO=OD.
Если проекции наклонных, проведённых из одной точки, равны, то равны и наклонные. Соответственно, ВК=КС=КD=KA (поскольку проекции данных наклонных (ВО, СО, DO и AO) равны между собой).
Найдём диагональ прямоугольника ABCD.
В прямоугольном ΔBAD (∠BAD=90°) по т. Пифагора:
BD²= AB²+AD²;
BD²= 12²+16²;
BD²= 400;
BD= 20 (-20 не подходит).
Диагонали прямоугольника равны, пересекаются и в точке пересечения делятся пополам => BO=OD=АО=ОD=½ BD= 20÷2=10 (см).
В прямоугольном ΔАОК (∠AOK=90°) по т. Пифагора:
АК²= АО²+ОК²;
АК²= 10²+(5√5)²;
AK²= 100+125;
AK²= 225;
AK= 15 (-15 не подходит).
Расстояние от т.К до вершин прямоугольника равно 15 см.
ОТВЕТ: 15 см.
P.S. Очень надеюсь, что все понятно расписала...)
У равнобедренного треугольника углы при основании равны.
1 вариант.
Угол при вершине в 4 раза больше угла при основании.Тогда:
Каждый угол при основании - х °
Угол при вершине - 4х°
х+х+4х= 180
6х=180
х=180 :6
х= 30° - каждый угол при основании
4×30°= 120 ° - угол при вершине
Это будет тупоугольный треугольник.
ответ: 30°,30°, 120°.
2 вариант.
Угол при основании в 4 раза больше, чем угол при вершине треугольника.
Угол при вершине - х °
Каждый угол при основании - 4х°
4х+4х+х= 180
9х=180
х=180 :9
х= 20° - угол при вершине
20×4 = 80° - каждый угол при основании треугольника.
Это остроугольный треугольник.
ответ: 20°, 80°, 80°.