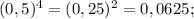
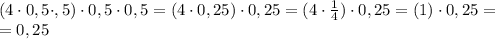
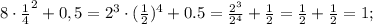
2) (6 + х)(х – 6) = х^2 - 36
3) (4в – 1)(4в + 1) = 16в^2 - 1
4) (х7 – а5)(х7 + а5) = х^14 - а^10
5) (0,3а3 + 0,2у4)(0,3а3 – 0,2у4) = 0,09а^6 - 0,04у^8
6) (х4 – в4)(х4 + в4)(х8 + в8) = х^16 - в^16
2) Упростить выражение: 1) (с + 2)(с – 2) – 4с(с - 1) = с^2 - 4 - 4с^2 + 4с = -3с^2 - 4 + 4с = -3с^2 + 4с - 4.2) (4а – 1)(4а + 1) + (9 + а)(а - 9) = 16а^2 - 1 + а^2 - 81 = 17а^2 - 82.
3) (с – 1)(6 – с) – (10 – с)(с + 10) = 6с - с^2 - 6 + с - 100 + с^2 = 7с - 106
3) Решить уравнение:1) (х + 3)(х – 3) –х(х + 4) = 0
х^2 - 9 - х^2 - 4х = 0
-9 - 4х = 0
-4х = 9
х = - 9/4
2) 3х(1 + 12х) – (6х – 1)(6х + 1) = 2,5х,
39 - 36х^2 + 1 = 5/2х
78х - 72х^2 + 2 = 5х
73х - 72х^2 + 2 = 0
-72х^2 + 73х + 2 = 0
72х^2 - 73х - 2 = 0

3) (х + 5)(х – 5) – (2х + 1)(х - 2) = 1 – х2.
х^2 - 25 - (2х^2 - 4х + х - 2) = 1 - х^2
х^2 - 25 - 2х^2 + 3х + 2 = 1 - х^2
- х^2 - 23 + 3х = 1 - х^2
- 23 + 3х = 1
3х = 24
х = 8
1) y=x+5 y=x²-1 S=?
x+5=x²-1
x²-x-6=0 D=24 √D=5
x₁=-2 x₂=3 ⇒
S=₋₂∫³( x+5-x²+1)dx=₋₂³(6+x-x²)dx=6x+x²/2-x³/3 ₋₂|³=
=6*3+3²/2-3³/3-(6*(-2)+(-2)²/2-(-2)³/3)=18+4,5-9-(-12+2-(-8/3))=
=13¹/₂+7¹/₃=20⁵/₆≈20,833.
ответ: S≈20,833 кв. ед.
2) y=2/x y=2 x=2 S=?
2/x=2
x=2/2=1. ⇒
S=₁²(2-2/x)dx=2x-2*lnx ₁|²=2*2-2*ln2-(2*1-ln1)=4-ln2²-2+0=2-ln4≈0,614.
ответ: S≈0,614кв. ед.