В решении.
Объяснение:
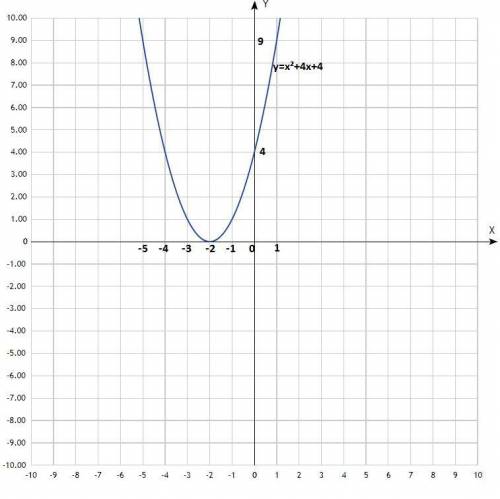
Постройте график функции у=х²+4х+4 и найдите координаты вершины параболы.
Дана функция у = х² + 4х +4;
Построить график.
Уравнение квадратичной функции, график - парабола со смещённым центром, ветви направлены вверх.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -5 -4 -3 -2 -1 0 1
у 9 4 1 0 1 4 9
По вычисленным точкам построить параболу.
Согласно графика, координаты вершины параболы: (-2; 0).
В решении.
Объяснение:
Решите уравнение.
7) х² + 4х = 5
↓
х² + 4х - 5 = 0
D=b²-4ac = 16 + 20 = 36 √D=6
х₁=(-b-√D)/2a
х₁=(-4-6)/2
х₁= -10/2
х₁= -5;
х₂=(-b+√D)/2a
х₂=(-4+6)/2
х₂=2/2
х₂= 1; В ответе х = -5;
8) х² - 6х = 16
↓
х² - 6х - 16 = 0
D=b²-4ac = 36 + 64 = 100 √D=10
х₁=(-b-√D)/2a
х₁=(6-10)/2
х₁= -4/2
х₁= -2;
х₂=(-b+√D)/2a
х₂=(6+10)/2
х₂=16/2
х₂= 8; В ответе х= -2;
9) х² + 2х = 15
↓
х² + 2х - 15 = 0
D=b²-4ac = 4 + 60 = 64 √D=8
х₁=(-b-√D)/2a
х₁=(-2-8)/2
х₁= -10/2
х₁= -5;
х₂=(-b+√D)/2a
х₂=(-2+8)/2
х₂=6/2
х₂= 3; В ответе х = -5;
10) х² - 7х = 8
↓
х² - 7х - 8 = 0
D=b²-4ac = 49 + 32 = 81 √D=9
х₁=(-b-√D)/2a
х₁=(7-9)/2
х₁= -2/2
х₁= -1;
х₂=(-b+√D)/2a
х₂=(7+9)/2
х₂=16/2
х₂= 8; В ответе х = -1.

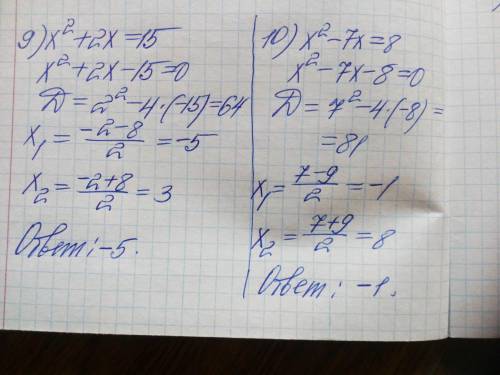
треугольник АВС, О-центр вписан.окруж., М-точка касания с гипотенузой АС, СМ=1, АМ=2, Е-точка касания с катетом ВС и К-точка касания с катетом АВ, СЕ=СМ=1 (отрезки, касательных к окружности, проведенных из одной точки), так же АК=АМ=2, ОЕ=ОК= радиусу окружности. ОЕ перпендикулярно к ВС (отрезок, проведенный от центра окружности к точке касания, перпендикю к данной стороне), также ОК перпендик. к ВА. угол АВС-90градусов. ВКОЕ-квадрат, где сторона равна радиусу и обозначим за х, тогда ВА=2+х, ВС=х+1, Ас=2+1=3-гипотенуза
По теореме Пифагора
(х+1)^2+(х+2)^2=3^2
x^2+2x+1+x^2+4x+4=9
2x^2+6x-4=0 сократим на 2
х^2+3x-2=0
дискрим Д=9+8=17
Х1=(-3+корень из 17)/2 (корень из 17 приблиз равен 4,12)
х2=(-3-корень из17)/2 (отрицат. быть не может)
ответ: радиус равен (-3+корень из 17)/2