В решении.
Объяснение:
а) 6x-x²<0
-x²+6x<0
Приравнять к нулю и решить как неполное квадратное уравнение:
-x²+6x=0
х²-6х=0
х(х-6)=0
х₁=0
х-6=0
х₂=6
Теперь начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное квадратное уравнение, ветви направлены вниз, парабола пересекает ось Ох при х= 0 и х=6, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у<0 (как в неравенстве), слева и справа от значений х, то есть, решения неравенства в интервале
х∈ (-∞, 0)∪(6, +∞).
Неравенство строгое, скобки круглые.
б)x²>81
Приравнять к нулю и решить как неполное квадратное уравнение:
x²=81
x₁,₂=±√81
x₁,₂=±9
x₁= -9
x₂=9
Снова начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное квадратное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -9 и х=9, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у>0 (как в неравенстве), слева и справа от значений х, то есть, решения неравенства в интервале
х∈ (-∞, -9)∪(9, +∞).
Неравенство строгое, скобки круглые.
в) 49х²>=36
Приравнять к нулю и решить как неполное квадратное уравнение:
49х²=36
x²=36/49
x₁,₂=±√36/49
x₁,₂=±6/7
x₁= -6/7
x₂=6/7
Снова начертим СХЕМУ параболы, которую выражает данное квадратное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -6/7 и х=6/7, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у>0 (как в неравенстве), слева и справа от значений х, то есть, решения неравенства в интервале
х∈ (-∞, -6/7]∪[6/7, +∞).
Неравенство нестрогое, скобка квадратная. Это значит, что значения х= -6/7 и х=6/7 входят в интервал решений неравенства.
У знаков бесконечности скобка всегда круглая.
г)x²-x+56>0
Приравнять к нулю и решить как полное квадратное уравнение:
x²-x+56=0
D=b²-4ac = 1-224 D<0, нет корней, нет решения у неравенства.
д)x²+4x+3<=0
Приравнять к нулю и решить как полное квадратное уравнение:
x²+4x+3=0
D=b²-4ac = 16-12=4 √D= 2
х₁=(-b-√D)/2a
х₁=(-4-2)/2
х₁= -6/2
х₁= -3
х₂=(-b+√D)/2a
х₂=(-4+2)/2
х₂= -2/2
х₂= -1
Снова начертим СХЕМУ параболы, которую выражает данное квадратное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -3 и х= -1, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у<=0 (как в неравенстве) при х от -3 до -1, то есть, решения неравенства находятся в интервале х∈ [-3, -1], причём значения х= -3 и х= -1 входят в решения неравенства.
Неравенство нестрогое, скобки квадратные.
е)x²-25<=0
Приравнять к нулю и решить как неполное квадратное уравнение:
x²-25=0
x²=25
x₁,₂=±√25
x₁,₂=±5
x₁= -5
x₂=5
Снова начертим СХЕМУ параболы, которую выражает данное квадратное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -5 и х= 5, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у<=0 (как в неравенстве) при х от -5 до 5, то есть, решения неравенства находятся в интервале х∈ [-5, 5], причём значения х= -5 и х= 5 входят в решения неравенства.
Неравенство нестрогое, скобки квадратные.
Объяснение:
{y⁴+19=20*(x+y) {y⁴+19=10*(2x+2y)
{√x+√(2x+x)=√2 {√x+√(2x+x)=√2 ОДЗ: х≥0.
Рассмотрим второе уравнение:
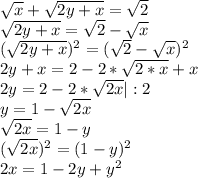
Подставляем 2х в первое уравнение:
y⁴+19=10*(1-2y+y²+2y)
y⁴+19=10+10y²
y⁴-10y²+9=0
Пусть у²=t≥0 ⇒
t²-10t+9=0 D=64 √D=8
t₁=y²=1 y₁=1 y₂=-1.
y₁=1 ⇒
2x=1-2*1+1²=0
x₁=0.
y₂=-1 ⇒
2x=1-2*(-1)+(-1)²=1+2+1=4
2x=4 |÷2
x₂=2.
t₂=y²=9 y₃=3 y₄=-3
y₃=3 ⇒
2x=1-2*3+3²=1-6+9=4
2x=4 |÷2
x₃=2.
y₄=-3 ⇒
2x=1-2(-3)+(-3)²=1+6+9=16
2x=16 |÷2
x₄=8.
Проверка показала, что корни системы уравнений х₃=2 у₃=3
и х₄=8 у₄=-3 лишние вследствие неоднократного возведения в степень второго уравнения.
ответ: x₁=0 y₁=1 x₂=2 y₂=-1.
5a + a^2 = 14
a^2 + 5a - 14 = 0
D = 25 + 56 = 81 = 9^2
a1 = ( - 5 + 9 ) : 2 = 2
a2 = ( - 5 - 9 ) : 2 = - 7
•••••••••••••
X/y = 2 ; x = 2y
X/y = - 7 ; x = - 7y
•••••••••••••
5x + 3y = 13
10y + 3y = 13
y = 1
X = 2
••••••••••••
5x + 3y = 13
- 35y + 3y = 13
- 32y = 13
y = - 13/32
X = ( - 7•13)/32 = - 91/32 = - 2 ( 27/32 )
ответ ( 2 ; 1 ) ; ( - 2 27/32 ; - 13/32 )