RayMiller avatar
не за что)
Реклама
Остались вопросы?
НАЙДИ НУЖНЫЙ
ЗАДАЙ ВОПРОС
Новые вопросы в Геометрия
дайте ответы на задачи
В треугольнике DFR провели прямую, параллельную стороне FR так, что она пересекает стороны DF и DR в точках S и Q , соответственно. Найди длину сторо…ны DR , если площадь треугольника DSQ равна 30 см ^2 , SQ = 5 см, DS = 12 см, FR =20 см.
В треугольнике MNK провели прямую, параллельную стороне MK так, что она пересекает стороны MN и KN в точках S и R , соответственно. Найди длину сторо…ны KN , если SN = 35 , NR= 28 , MN = 80,5 .
В треугольнике ABC сторона BC=47см из вершины A проведена медиана AM Чем будет равен отрезок BM
Даны параллельные прямые m и n, <ABC=26, <DEK=57 Найдите чему равен <BDE Умоляю
Велосипедист ( ). Малыш на 10-дюймовом велосипеде катается по квартире. До поворота ему осталось 5 метров. Сколько оборотов сделают колеса до по…ворота? Число п считай приближенно равным мне надо ((
тест решить 20б
Применяя соотношения в прямоугольном треугольнике, решите задачу по рисункам
Диагонали трапеции ABCD с основаниями AB и CD пересекаются в точке O.Найти BD если известно, что OB=18, AB=34, DC=102
ПОКАЗАТЬ ЕЩЕ
Предыдущий
Следующий
Задай вопр
Объяснение:
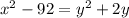
Заметим, что если в правой части добавить 1, то получим формулу квадрата суммы. Тогда, добавим 1 и в левой и в правой части:
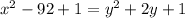
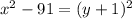
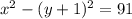
Применим формулу разности квадратов:
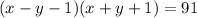
Заметим, что если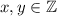 
, то обе скобки, записанные в левой части, дают целые числа.
Разложим число 91 на простые множители:
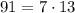
Тогда, число 91 можно получить путем умножения либо чисел 7 и 13, либо чисел 1 и 91. Нужно учесть, что эти числа могут умножаться в разных порядках, а также то, что оба множителя могут поменять знак на противоположный.
Таким образом есть 8 упорядоченных пар целых чисел, в произведении дающих 91:
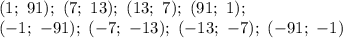
Но данные пары целых чисел соответствуют скобкам в произведении 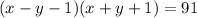. Необходимо проверить, будут ли сами числа 
и 
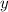в каждом из этих случаев целыми. Можно составить и решить 8 систем, но вместо этого мы составим одну систему в общем виде, решим ее опять же в общем виде и проанализируем результаты.
Рассмотрим систему:
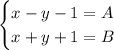
Пусть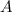 
и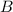 
- целые числа. Решим систему методом сложения. Сложив уравнения, получим:
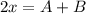
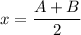
Заметим, что является целым числом, когда 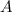и 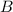имеют одинаковую четность.
Из второго уравнения выразим :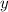
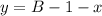
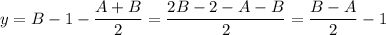
Аналогично, 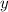является целым числом, когда 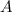и 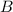имеют одинаковую четность.
Но все числа в наших парах:
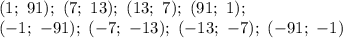
имеют одинаковую четность. Значит, все 8 систем дадут по одному решению в целых числах. Таким образом, исходное уравнение имеет 8 решений в целых числах.
ответ: 8
