Если точки M, N и P лежат на одной прямой, то расстояние межу крайними точка М и Р должно равняться сумме отрезков МN и NP (см рисунок 1)
Тогда
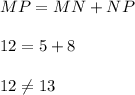
Отсюда можно сделать вывод: точки M, N и P НЕ лежат на одной прямой (см. рисунок 2)
сокращать(округлять) десятичные дроби можно до десятых-один знак после запятой, сотых- два знака, тысячных- три знака и дальше соответственно.
твоё число 156,79571212, сократим до сотых. следовательно, у нас после запятой должно остаться 2 циферки. Теперь, внимание, алгоритм. Смотрим на цифру, стоящую после, тех самых двух что должны остаться(Х). В нашем случае Х это 5. Так вот, ели это цифра Х меньше 5 (0,1,2,3,4), то те самые две циферки после запятой прямиком как есть идут в ответ, если же цифра Х равна 5 или больше (5,6,7,8,9) прибавляем к нашему числу из двух знаков единицу. Это и будет ответом.
156,79571212 до сотых = 156,80 (до сотых, след 2 цифры после запятой; 5,след. +1; 79+1=80)
НЕТ, не лежат на одной привет.
Отрезок MP должен быть равен сумме отрезков MN и NP.
MN +NP = 5+8 = 13 ≠ MP = 12.
Рисунок к задаче в приложении.