![( \sqrt{z} +2)*(z-2 \sqrt{z} +4)= [( \sqrt{z}) +(2)]*[( \sqrt{z} )^2-(\sqrt{z})*(2) +(2)^2]=](/tpl/images/0617/5186/4e37d.png)
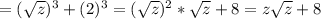
![( \sqrt{2} -2\sqrt{s})*(2+2 \sqrt{2s} +4s)= [( \sqrt{2}) -(2\sqrt{s})]*[( \sqrt{2} )^2+(\sqrt{2})*(2\sqrt{s}) +(2\sqrt{s})^2]=](/tpl/images/0617/5186/a352c.png)
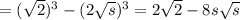
Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)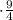 - объем работы системы из двух насосов за 2ч 15мин.
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение: 
9t = 1

Значит, 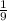 - цис./ч - производительность "медленного" насоса.
- цис./ч - производительность "медленного" насоса.
Тогда 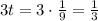 - цис./ч - производительность "быстрого" насоса.
- цис./ч - производительность "быстрого" насоса.
Следовательно, 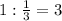 ч - потребуется "быстрому" насосу на заполнение цистерны.
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.




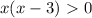
 ∈
∈ 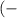 ∞
∞  ∪
∪ 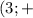 ∞
∞ 

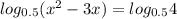
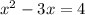
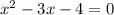
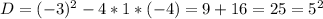
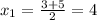
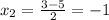


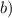

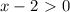
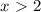
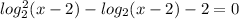

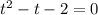

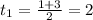

 или
или 
 или
или 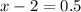
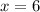 или
или 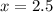

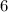
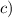
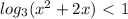

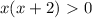
 ∈
∈ 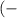 ∞
∞  ∪
∪ 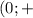 ∞
∞ 

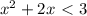


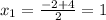

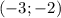 ∪
∪