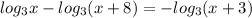
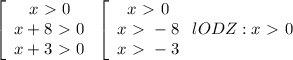
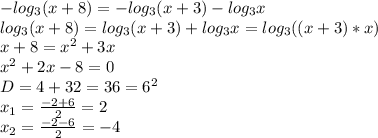
противоречит ОДЗ, а потому не является решением.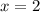 
ax² + bx + c = 0 - квадратное уравнение (a ≠ 0), называется неполным, если b = 0, или c = 0, или оба сразу (b = 0 и c = 0). Разберем все эти случаи.
1) b = 0 и c ≠ 0
ax² + c = 0
ax² = -c
x² = -c / a
x² ≥ 0, поэтому для того, чтобы уравнение не имело корней достаточно -c / a < 0; c / a > 0 - получили ответ на первый вопрос
2) b ≠ 0; c = 0
ax² + bx = 0
x·(ax + b) = 0
x₁ = 0; x₂ = -b / a
То есть корни будут всегда, и мы получили ответ на второй вопрос задачи:
(при b ≠ 0; c = 0; Уравнение ax² + bx = 0 имеет 2 корня, один из которых 0)
3) b = 0 и c = 0
ax² = 0
x = 0, то есть всегда корнем будет 0
Объяснение:
ответ:
объяснение:
здесь область допустимых значений состоит только из двух
под первым корнем квадратный трехчлен --парабола, ветви вверх:
2x²-8x+6 ≥ 0
x²-4x+3 ≥ 0 корни: 1 и 3 (по теореме виета)
решение: х ∈ (-∞; 1] u [3; +∞)
под вторым корнем квадратный трехчлен --парабола, ветви вниз:
-x²+4x-3 ≥ 0
x²-4x+3 ≤ 0 корни те же))
решение: х ∈ [1; 3]
пересечением этих двух промежутков (условия должны выполняться одновременно) будет множество из двух точек: х ∈ {1; 3}
легко проверить, что х=1 решением не является, т.к. сумма двух неотрицательных чисел (это квадратные корни) не может быть < 1-1 (меньше нуля)
остается х = 3: √0 + √0 < 3-1 это верно))
ответ: х=3
