Примем --- м=100книг
Х- количество книг на одной полоке
м:х=100:х=100/х - количество полок вначале
м:(х+5)=100/(х+5) - количество полок
(100/х) - 100/(х+5) =2
(100/х) - 100/(х+5) -2=0 -- общий знаменатель х*(х+5)
100*(х+5) -100*х -2*х*(х+5)=0
100х+500-100х -2х² - 10х=0
-2х²-10х+500=0 - квадратное уравнение
Д=(-10)²-4*(-2)*500=100+4000=4100
Х1= (-(-10)-√4100) : 2*(-2)= -54,03:(-4)=13,5 =14 книг на одной полке (округлили до ближайшего целого числа)
Х2= (-(-10)+√4100) : 2*(-2)= 74:(-4)=13,5 = -18,5 -не подходит т.к. с минусом
Проверка:
100:14=7,14 =8 полок
100:(14+5)=100:19=5,2=6 полок
8-6=2 полки - верно
ответ: на 8 полках размещены учебники
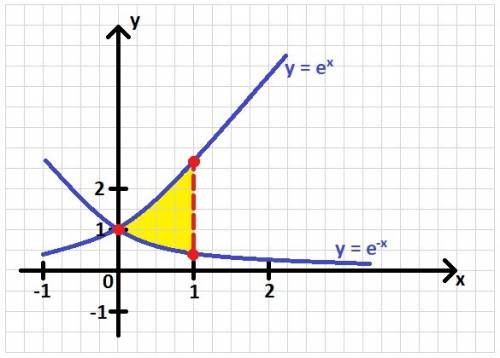
Для решения задачи в первую очередь нужно построить график.
По графику видно, что найти нужно площадь области, лежащей над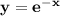 
и под 
.
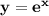Найдём точку пересечения данных кривых. Для этого нужно решить систему из уравнений их функций.
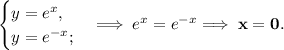
По графику прямая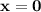 
будет являться границей фигурой слева, а прямая 
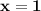— справа.
Найти площадь фигуры, ограниченной сверху графиком функции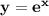 
, а снизу функцией 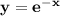, а так же прямым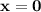и и 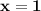, значит вычислить следующий определённый интеграл.
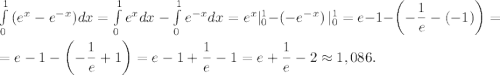
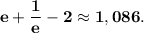
Для пересечения выпиши только те буквы, которые встречаются в обеих пословицах, то есть, и в первой и во второй одновременно. Например, буква "ч" в пересечение не войдет, потому что она входит только в множество букв второй пословицы, а в множество букв первой пословицы - не входит.