ответ: Отношение скорости мотоциклиста к скорости велосипедиста равно 2
Объяснение:
Обозначим расстояние между велосипедистами за S Vb-скорость велосипедиста велосипедиста ; Vm-скорость мотоциклиста Теперь если они едут на встречу друг-другу мы должны разделить расстояние между ними (S) на сумму их скоростей То есть : S:(Vb+Vm)=1 ч 20 =
чИ так же нам известно что они идут в одном направление ; и то что мотоциклист догонит велосипедиста через 4 часа это значит что Vm > Vb Так как они идут в одном направлении расстояние между ними нужно разделить на разность их скоростей То есть : S:(Vm-Vb)=4 ч Составим систему :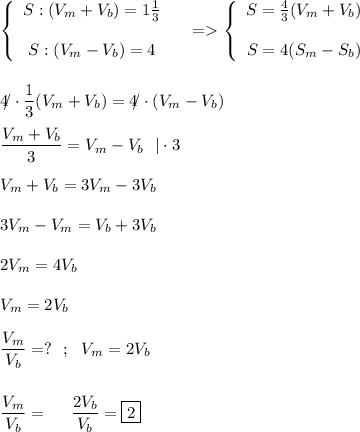 
В решении.
Объяснение:
Решить неравенство:
1) 2х + 5 > 7x - 10
2x - 7x > -10 - 5
-5x > - 15
5x < 15 знак неравенства меняется при делении на минус
x < 15/5
x < 3;
Решение неравенства: х∈(-∞; 3).
Неравенство строгое, скобка круглая, а знаки бесконечности всегда с круглой скобкой.
2) 2(3х + 7) - 8(х + 3) <= 0
6x + 14 - 8x - 24 <= 0
-2x - 10 <= 0
-2x <= 10
2x >= -10 знак неравенства меняется при делении на минус
x >= -5;
Решение неравенства: х∈[-5; +∞).
Неравенство нестрогое, скобка квадратная, а знаки бесконечности всегда с круглой скобкой.
3) (х + 3)/4 - х/2 >= 3
Умножить все части неравенства на 4, чтобы избавиться от дроби:
х + 3 - 2х >= 12
-x >= 12 - 3
-x >= 9
x <= -9 знак неравенства меняется при делении на минус
Решение неравенства: х∈(-∞; -9].
Неравенство нестрогое, скобка квадратная, а знаки бесконечности всегда с круглой скобкой.
Решить систему неравенств:
1) 3 - х <= 5
4x - 2 < 8
-x <= 5 - 3
4x < 8 + 2
-x <= 2
4x < 10
x >= -2 знак неравенства меняется при делении на минус
x < 2,5
Решение первого неравенства: х∈[-2; +∞);
Решение второго неравенства: х∈(-∞; 2,5).
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем значения - бесконечность, -2, 0, 2,5, + бесконечность.
х∈[-2; +∞) - штриховка от -2 вправо до + бесконечности, кружок у -2 закрашенный.
х∈(-∞; 2,5) - штриховка от - бесконечности вправо до 2,5.
Пересечение х∈[-2; 2,5) (двойная штриховка), это и есть решение системы неравенств.
2) 2(х + 3) - 3(х - 2) > 0
2x + 3(2x - 3) <= 7
2x + 6 - 3x + 6 > 0
2x + 6x - 9 <= 7
-x + 12 > 0
8x - 9 <= 7
-x > -12
8x <= 16
x < 12 знак неравенства меняется при делении на минус
x <= 2
Решение первого неравенства: х∈(-∞; 12);
Решение второго неравенства: х∈(-∞; 2].
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем значения - бесконечность, 0, 2, 12.
х∈(-∞; 12) - штриховка от - бесконечности вправо до 12.
х∈(-∞; 2] - штриховка от - бесконечности вправо до 2, кружок у 2 закрашенный.
Пересечение х(-∞; 2] (двойная штриховка), это и есть решение системы неравенств.
=а(2²-а²)=а(2-а)(2+а)