
1. Область определения функции — множество всех действительных чисел.
2. Множество значений функции:
Так как синус изменяется от -1 до 1, то оценивая в виде двойного неравенства, имеем
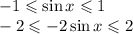
Множество значений функции y=-2sinx: отрезок [-2;2].
3. Функция периодическая с периодом T = 2π
4. Функция нечетная , так как y(-x) = 2sin x = -y(x)
5. Наибольшее значение, равное 2, при 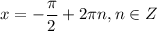
Наименьшее значение, равное -2, при 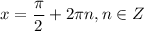
6. Функция возрастает на отрезке ![\bigg[-\dfrac{3\pi}{2};-\dfrac{\pi}{2}\bigg]](/tpl/images/0199/1232/9b9b9.png) и на отрезках, получаемых сдвигами этого отрезка на
и на отрезках, получаемых сдвигами этого отрезка на 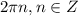
убывает на отрезке ![\bigg[-\dfrac{\pi}{2};\dfrac{\pi}{2}\bigg]](/tpl/images/0199/1232/aa45e.png) и на отрезках, получаемых сдвигами этого отрезка на
и на отрезках, получаемых сдвигами этого отрезка на 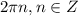
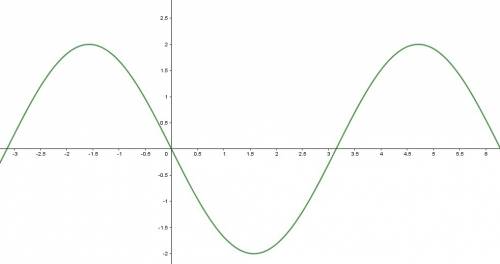
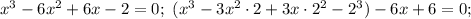
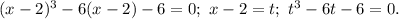
Докажем сначала, что корень единственный. Для этого исследуем функцию 
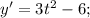 корни производной
корни производной 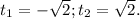
В точке  функция имеет локальный максимум, в точке
функция имеет локальный максимум, в точке 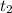 - локальный минимум, после него функция монотонно растет.
- локальный минимум, после него функция монотонно растет.
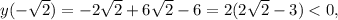 так как корень из двух меньше, чем 1,5. Итак, слева от
так как корень из двух меньше, чем 1,5. Итак, слева от  функция возрастает, справа убывает, начиная с
функция возрастает, справа убывает, начиная с 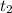 снова возрастает. Поскольку функция в точке
снова возрастает. Поскольку функция в точке  отрицательна, существует только один корень функции (и расположен он правее
отрицательна, существует только один корень функции (и расположен он правее 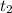 ; для нас, правда, важна только его единственность).
; для нас, правда, важна только его единственность).
Возвращаемся к уравнению  Для его решения применим метод Кардано. Замена
Для его решения применим метод Кардано. Замена 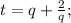 после элементарных упрощений получаем уравнение
после элементарных упрощений получаем уравнение 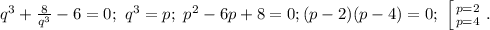
Вроде бы надо исследовать оба значения p, однако оба они дадут одно и то же значение t (кстати, ранее мы даже доказали, что двух решений быть не может). Итак, пусть p=2; ![q=\sqrt[3]{2};\ t=\sqrt[3]{2}+\frac{2}{\sqrt[3]{2}}=\sqrt[3]{2}+\sqrt[3]{4}; x=2+\sqrt[3]{2}+\sqrt[3]{4}](/tpl/images/0199/1839/61451.png)
ответ: ![2+\sqrt[3]{2}+\sqrt[3]{4}](/tpl/images/0199/1839/f6929.png)