Надо! 3x-5/7 + 2х+1/14 +2х-3/2 /-это знак деления. всё это дроби. в числителе 3х-5,а в знаменателе 7

👇

Ответ:

Gykplhgv

05.02.2023

Общий знаменатель 14

=(2(3x-5) +2x+1 +7(2x-3)) /14 =

=(6x -10 +2x +1 +14x -21) /14 =

=(22x -30) /14 =2(11x -15) /14 =(11x -15) /7

4,4(7 оценок)

Открыть все ответы

Ответ:

makaroshkaplay

05.02.2023

1) Безболезненно возводим все в квадрат, получим (x^2-5x)^2=(4x)^2

(x^2-5x-4x)(x^2-5x+4x)=0

x=0, 1, 9

2) Уравнение квадратное относительно |x|=t: t^2-6t+5=0, t=5 or 1; x=+-1,+-5

3) Можно опять возвести в квадрат или записать совокупность. Так или иначе, x^2-5x+-6=0. x=2,3,6,-1

4) Тут можно и геометрическим смыслом модуля попользоваться. Сумма расстояний от x^2 до точек 4 и 9 равно 12. Отсюда либо точка x^2 правее 9 (тогда x^2=12,5), либо точка левее 4 (тогда x^2=0.5). x=+-sqrt(2)/2, +-5sqrt(2)/2

4,4(48 оценок)

Ответ:

Макс332211

05.02.2023

Функция
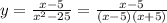
$y= \frac{x-5}{x^2-25} = \frac{x-5}{(x-5)(x+5)}$
определена на всей числовой оси, кроме двух точек: x = -5 и x = 5.

Найдём односторонние пределы в этих точках.

1) x = -5. Т.к. в этой точке множитель (x-5) не равен нулю, то его можно сократить.
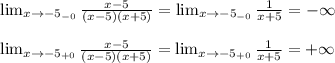
$\lim_{x \to \inft{-5_{-0}}} \frac{x-5}{(x-5)(x+5)} =\lim_{x \to \inft{-5_{-0}}} \frac{1}{x+5} =-\infty \\ \\ \lim_{x \to \inft{-5_{+0}}} \frac{x-5}{(x-5)(x+5)} =\lim_{x \to \inft{-5_{+0}}} \frac{1}{x+5} =+\infty$

Оба односторонних предела бесконечны, значит, функция терпит разрыв II рода в точке x = -5. Кстати, уравнение x = -5 есть уравнение вертикальной асимптоты в точке разрыва.

2) x = 5. В этой точке множитель (x + 5) равен 10.
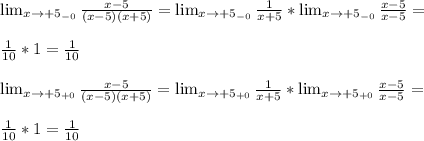
$\lim_{x \to \inft{+5_{-0}}} \frac{x-5}{(x-5)(x+5)} =\lim_{x \to \inft{+5_{-0}}} \frac{1}{x+5} *\lim_{x \to \inft{+5_{-0}}} \frac{x-5}{x-5}= \\ \\ \frac{1}{10} *1=\frac{1}{10} \\ \\ \lim_{x \to \inft{+5_{+0}}} \frac{x-5}{(x-5)(x+5)} =\lim_{x \to \inft{+5_{+0}}} \frac{1}{x+5} *\lim_{x \to \inft{+5_{+0}}} \frac{x-5}{x-5}= \\ \\ \frac{1}{10} *1=\frac{1}{10}$

В точке x = 5 функция терпит разрыв, т.к. на ноль делить нельзя. Однако односторонние пределы конечны, следовательно, это точка разрыва I рода. При этом односторонние пределы совпадают, справа и слева значение функции бесконечно приближается к 1/10. Значит, этот разрыв устранимый.
Итак, в точке x = 5 функция терпит устранимый разрыв I рода.

Из выше изложенного можно сделать некоторые представления о графике нашей функции. Во-первых, функция слева направо бесконечно убывает, приближаясь к точке х = -5. Во-вторых, справа от точки х = - 5 функция убывает из плюс бесконечности. В точке х = 5 она терпит устранимый разрыв, продолжая дальше убывать.
Найдём горизонтальные асимптоты.
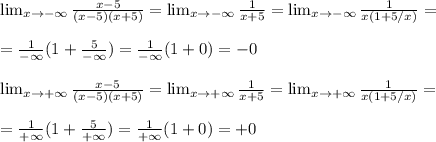
$\lim_{x \to -\infty} \frac{x-5}{(x-5)(x+5)}=\lim_{x \to -\infty} \frac{1}{x+5}= \lim_{x \to -\infty} \frac{1}{x(1+5/x)}= \\ \\ = \frac{1}{-\infty}(1+ \frac{5}{-\infty}} )}=\frac{1}{-\infty}(1+ 0)}=-0 \\ \\ \lim_{x \to +\infty} \frac{x-5}{(x-5)(x+5)}=\lim_{x \to +\infty} \frac{1}{x+5}= \lim_{x \to +\infty} \frac{1}{x(1+5/x)}= \\ \\ = \frac{1}{+\infty}(1+ \frac{5}{+\infty}} )}=\frac{1}{+\infty}(1+ 0)}=+0$

Горизонтальная асимптота y = 0. Функция бесконечно приближается к нулю, влево, в минус бесконечность, снизу, справа, в плюс бесконечность, сверху.

* Функция непрерывна при x ∈(-∞; -5) ∪ (-5; 5) ∪ (5; +∞).
* В точке x = -5 разрыв II рода, в точке x = 5 устранимый разрыв I рода.

4,6(31 оценок)

Это интересно:

Взаимоотношения

27.11.2022

Как познакомиться с женщинами где угодно: советы от профессионалов...

Питомцы-и-животные

04.01.2023

Как правильно ухаживать за щенком английского бульдога?...

Компьютеры-и-электроника

08.07.2022

Как построить боевого робота класса Antweight...

Образование-и-коммуникации