Решить с решением: десятиклассники измеряли длину шага.получены результаты (в см.) 68,63,73,67,75. найдите среднее арифметическое и размах ряда полученных данных.

👇

Увидеть ответ

Ответ:

Groza11

15.07.2020

Среднее арифметическое находится так: складываются все числа и делятся на количество.
68+63+73+67+75=346
346/5=69,2

4,4(85 оценок)

Ответ:

didi20023

15.07.2020

Среднее арифметическое 68

4,6(92 оценок)

Открыть все ответы

Ответ:

tim20053

15.07.2020

ответ: 286,5 см².

Объяснение:

Дано. ABCD - прямоугольная трапеция.

BD - диагональ является биссектриса острого угла.

найдите площадь трапеции, если боковые стороны равны 10 см и 20 см.

Решение.

Биссектриса в трапеции отсекает равнобедренный треугольник.

ВС=CD=20 см.

Проведем высоту СЕ. Из треугольника CED:

DE=√20²-10²=√400-100=√300 = 10√3 =17,3 см. Тогда

основание AD=AE+ED=20+17,3 = 37,3 см.

Площадь трапеции S=h(a+b)/2 = 10(20+37,3)/2=10*57,3/2=286,5 см².

Площадь трапеции равна 286,5 см².

4,4(88 оценок)

Ответ:

Danfdffefd

15.07.2020

Исходное неравенство распадается на совокупность систем:

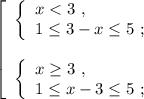
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ 1 \leq 3-x \leq 5 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 1 \leq x-3 \leq 5 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ -5 \leq x-3 \leq -1 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 1+3 \leq x \leq 5+3 \ ; \end{array}\right \end{array}\right$

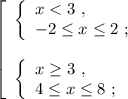
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ -2 \leq x \leq 2 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 4 \leq x \leq 8 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} x \in [ -2 ; 2 ] \ , \\ x \in [ 4 ; 8 ] \ ; \end{array}\right$

$x \in [ -2 ; 2 ] \cup [ 4 ; 8 ] \ ;$

а) неравенство эквивалентно:

$-2 \leq x \leq 2 \ ;$

$x \in [ -2 ; 2 ] \ ;$

Отрезок данного решения полностью совпадает с одним из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет 1/2 .

о т в е т :    $\frac{1}{2} = 0.5 = 50 \% \ ;$

б) неравенство эквивалентно:

$-2 \leq x-6 \leq 2 \ ;$

$6-2 \leq x \leq 2+6 \ ;$

$x \in [ 4 ; 8 ] \ ;$

Отрезок данного решения полностью совпадает с одним из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет 1/2 .

о т в е т :    $\frac{1}{2} = 0.5 = 50 \% \ ;$

в) неравенство эквивалентно:

$-1 \leq x \leq 1 \ ;$

$x \in [ -1 ; 1 ] \ ;$

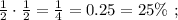
Отрезок данного решения составляет половину от одного из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет    $\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4} = 0.25 = 25 \% \ ;$

о т в е т :    $\frac{1}{4} = 0.25 = 25 \% \ ;$

г) неравенство распадается на совокупность систем:

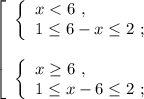
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ 1 \leq 6-x \leq 2 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 1 \leq x-6 \leq 2 \ ; \end{array}\right \end{array}\right$

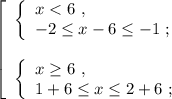
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ -2 \leq x-6 \leq -1 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 1+6 \leq x \leq 2+6 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ 4 \leq x \leq 5 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 7 \leq x \leq 8 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} x \in [ 4 ; 5 ] \ , \\ x \in [ 7 ; 8 ] \ ; \end{array}\right$

$x \in [ 4 ; 5 ] \cup [ 7 ; 8 ] \ ;$

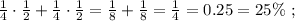
Каждый из двух отрезков данного решения составляет четверть от одного из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет    $\frac{1}{4} \cdot \frac{1}{2} + \frac{1}{4} \cdot \frac{1}{2} = \frac{1}{8} + \frac{1}{8} = \frac{1}{4} = 0.25 = 25 \% \ ;$

о т в е т :    $\frac{1}{4} = 0.25 = 25 \% \ ;$

4,4(14 оценок)

Это интересно:

Дом-и-сад

16.05.2021

Как избавиться от пятен после постельных клопов...

Компьютеры-и-электроника

29.01.2023

О преобразовании файлов ODT в DOC и почему это важно...

Мир-работы

29.12.2021

Как успешно пройти тестирование при приеме на работу...

03.04.2021