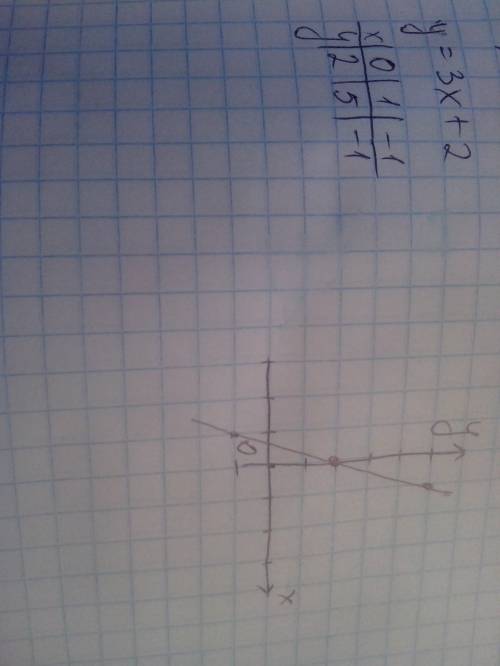
найдем одз. под корнем может находиться только неотрицательное значение, значит 5-х> =0, откуда х< =5. корень может принимать только неотрицательные значения, значит 5-х^2> =0, откуда х^2< =5, откуда |х|< =√5, откуда -√5< =х< =√5.
теперь решение:
вoзведем в квадрат:
(5-x^2)^2=5-x
25-10x^2+x^4=5-x
x^4-10x^2+x+20=0
(x^2-x-4)(x^2+x-5)=0
1) x^2-x-4=0
d=17
x(1)=(1+√17)/2> (1+√16)/2=(1+4)/2=5/2=√5*√5/2> √5*√4/2=√5. значит этот корень не подходит.
x(2)=(1-√17)/2 подставляя в изначальное уравнение, проверяем, что этот корень подходит.
2) x^2+x-5=0
d=21
x(1)=(-1+√21)/2 подставляя в изначальное уравнение, проверяем, что этот корень подходит.
x(2)=(-1-√21)/2< (-1-√16)/2=-5/2=-√5*√5/2< -√5*√4/2=-√5. значит этот корень не подходит.
ответ: х(1)=(1-√17)/2, х(2)=(-1+√21)/2.
Степень многочлена - наибольшая из степеней входящих в многочлен одночленов. Степень многочленов можно определить только после его приведения к стандартному виду, то есть к такому виду, когда все входящие в него одночлены приведены к стандартному виду, а подобных членов нет.
Данный многочлен 7 * x^2 * y^5 - 6 * x^6 + 8 * x^5 приведён к стандартному виду. Определим его степень:
Степень первого одночлена 7 * x^2 * y^5 равна 2 + 5 = 7; второго одночлена - 6 * x^6 равна 6; третьего одночлена 8 * x^5 равна 5.
Следовательно, степень многочлена равна 7, так как это наибольшая степень.
Объяснение: