a) D(x) = (-∞; +∞)
б) D(x) = (-∞;0) U (0;+∞)
Объяснение:
Область определения функции - это те значения аргумента (х), при которых СУЩЕСТВУЕТ функция.
Другими словами, если вы хотите найти область определения функции, то это значит найти значения х.
В наших случаях:
а)
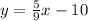
Это линейная функция. Аргумент (х) не имеет ограничений (не стоит в знаменателе , под знаком корня).
Поэтому : x - любое число, или
D(x) = (-∞; +∞)
б)
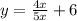
В этой функции мы видим х в знаменателе. Значит функция будет существовать при всех значениях аргумента (х), кроме 0, т.е
5х≠0
х≠0
получаем:
D(x) = (-∞;0) U (0;+∞)
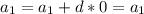проверено.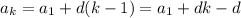
![a_{k+1}=a_1+d[(k+1)-1]=a_1+dk](/tpl/images/0582/6750/35dc7.png)
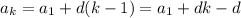то прибавив к данному выражению d. Мы получим следующий член .![S_n= \frac{n[2a_1+d(n-1)]}{2}](/tpl/images/0582/6750/67d86.png)
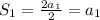. ![n=k \Rightarrow S_k= \frac{k[2a_1+d(k-1)]}{2}= \frac{2a_1k+dk^2-dk}{2}](/tpl/images/0582/6750/b9ca4.png)
:
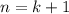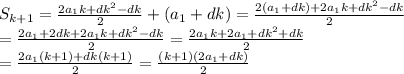
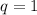получается деление на ноль, поэтому сразу пишем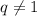 
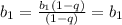
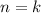
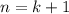:![b_{k+1}= \frac{b_1(1-q^k)}{1-q}+b_1q^k= \frac{(1-q)b_1q^k+b_1(1-q^k)}{1-q}\\= \frac{b_1[(1-q)q^k+(1-q^k)]}{1-q}= \frac{b_1[q^k-q^{k+1}+1-q^k]}{1-q}= \frac{b_1(1-q^{k+1})}{1-q}](/tpl/images/0582/6750/552be.png)
1)7:21/24=24/3=8
2)0,8-4/5=4/5-4/5=0
3)0+8=8
ответ. 8
Во втором задании -Всего спортсменов - 10. Из Норвегии - 1 спортсмен. Тогда вероятность равна 1/10, т.е. 0,1 (10%)